有一面积为1平方米的正方形纸,第一次剪掉一半,第二次剪掉剩下的一半,如此下去,第5次后剩下的纸面积是多少平方米?
如图是一个半圆形桥洞截面示意图,圆心为O, 直径AB是河底线,弦CD是水位线,CD∥AB,且CD =" 24"
直径AB是河底线,弦CD是水位线,CD∥AB,且CD =" 24"  m.已测得水面距桥洞最高处有8m
m.已测得水面距桥洞最高处有8m
(即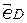 中点到CD的距离)
中点到CD的距离)
求半径OA;
根据需要,水面要以每小时0.5 m的速度
下降,则经过多长时间才能将水排干?
如图所示,在⊙O中,AB是直径,CD是弦,AB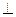 CD,AB=12cm.
CD,AB=12cm.
F是
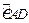 上一点(不与C、D
上一点(不与C、D 重合),求证:∠CFD=∠COB;
重合),求证:∠CFD=∠COB;若∠CFD=60
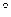 ,求CD的长
,求CD的长
某种商品,按标价销售每件可盈利50元,平均每天销售24件,根据市场信息,若每件降价2元,则每天可多销售6件,如果经销 商想保证每天盈利2160元,同时考虑不过多增加营业员的工作量,即每天销售不超过100件,每件商品应降价多少元
商想保证每天盈利2160元,同时考虑不过多增加营业员的工作量,即每天销售不超过100件,每件商品应降价多少元 ?
?
解方程5x(x+3)=2(x+3)
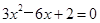
如图①,在正方形ABCD中,点E、F分别为边BC、CD的 中点,AF、DE相交于点G,则可得结论:①AF=DE,②AF⊥DE。(不需要证明)
中点,AF、DE相交于点G,则可得结论:①AF=DE,②AF⊥DE。(不需要证明)
如图②,若点E、F不是正方形ABCD的边BC、CD的中点,但满足CE=DF。则上面的结论①、②是否仍然成立?(请直接回答“成立”或“不成立”)
如图③,若点E、F分别在正方形ABCD的边CB的延长线和D
 C的延长线上
C的延长线上 ,且CE=DF,此时上面的结论①、②是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由。
,且CE=DF,此时上面的结论①、②是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由。如图④,在(2)的基础上,连接AE和EF,若点M、N、P、Q分别为AE、EF、FD、AD的中点,请判断四边形MNPQ是“矩形、菱形、正方形、等腰梯形”中的哪一种?
 并写出证明过程。
并写出证明过程。