如图,已知四棱锥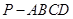 底面
底面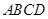 为菱形,
为菱形,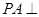 平面
平面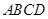 ,
,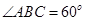 ,
, 分别是
分别是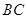 、
、 的中点.
的中点.
(1)证明:
(2)设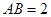 , 若
, 若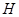 为线段
为线段 上的动点,
上的动点,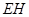 与平面
与平面 所成的最大角的正切值为
所成的最大角的正切值为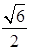 ,求此时异面直线AE和CH所成的角.
,求此时异面直线AE和CH所成的角.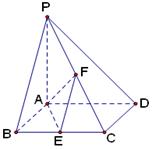
设 在
在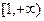 上是单调函数.
上是单调函数.
(1)求实数 的取值范围;
的取值范围;
(2)设 ≥1,
≥1, ≥1,且
≥1,且 ,求证:
,求证: .
.
双曲线E经过点A(4,6),对称轴为坐标轴,焦点F1,F2在X轴上,离心率e=2。
(1)求双曲线E的方程;
(2)求∠F1AF2的角平分线所在直线的方程.
定义在R上的函数f(x)满足f(x+2)=-f(x),且当x∈[-1,1]时,f(x)=x3.
(1)求f(x)在[1,5]上的表达式;
(2)若A={x| f(x)>a, x∈R},且A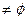 ,求实数a的取值范围.
,求实数a的取值范围.
为了对某课题进行讨论研究,用分层抽样的方法从三所高校A,B,C的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人)
| 高校 |
相关人数 |
抽取人数 |
| A |
X |
1 |
| B |
36 |
y |
| C |
54 |
3 |
(1)求x,y;
(2)若从高校A,C 抽取的人中选2人作专题发言,求这两人都来自高校C的概率.
记函数f(x)=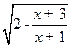 的定义域为A,
的定义域为A,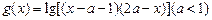 的定义域为B.
的定义域为B.
(1)求集合A;
(2)求集合B.