小李上山速度为mkm/h(h为小时),下山速度为nkm/h,求他的平均速度。
某工厂计划生产A、B两种产品共10件,其生产成本和利润如下表:
| A种产品 |
B种产品 |
|
| 成本(万元/件) |
2 |
5 |
| 利润(万元/件) |
1 |
3 |
(1)若工厂计划获利14万元,问A、B两种产品应分别生产多少件?
(2)若工厂计划投入资金不多于44万元,且获利多于14万元,问工厂有哪几种生产方案?
(3)在(2)的条件下,哪种生产方案获利最大?并求出最大利润。
近几年兴义市加大中职教育投入力度,取得了良好的社会效果。某校随机调查了九年级a名学生升学意向,并根据调查结果绘制如图的两幅不完整的统计图。
请你根据图中信息解答下列问题:
(1)a=;
(2)扇形统计图中,“职高”对应的扇形的圆心角α=;
(3)请补全条形统计图;
(4)若该校九年级有学生900名,估计该校共有多少名毕业生的升学意向是职高。
如图,△ABC内接于⊙O,AB=8,AC=4,D是AB边上一点,P是优弧 的中点,连接PA、PB、PC、PD,当BD的长度为多少时,△PAD是以AD为底边的等腰三角形?并加以证明。
的中点,连接PA、PB、PC、PD,当BD的长度为多少时,△PAD是以AD为底边的等腰三角形?并加以证明。
(1)计算:
(2)解方程: .
.
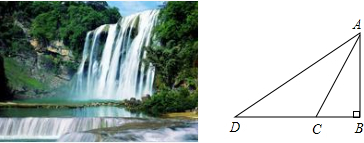
小亮想知道亚洲最大的瀑布黄果树夏季洪峰汇成巨瀑时的落差.如图,他利用测角仪站在C处测得∠ACB=68°,再沿BC方向走80m到达D处,测得∠ADC=34°,求落差AB.(测角仪高度忽略不计,结果精确到1m)