下表为某月的月历。
| 日 |
一 |
二 |
三 |
四 |
五 |
六 |
| |
|
1 |
2 |
3 |
4 |
5 |
| 6 |
7 |
8 |
9 |
10 |
11 |
12 |
| 13 |
14 |
15 |
16 |
17 |
18 |
19 |
| 20 |
21 |
22 |
23 |
24 |
25 |
26 |
| 27 |
28 |
29 |
30 |
31 |
|
|
(1)在此月历上用一个矩形任意圈出2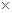 3个数,如果圈出的6个数之和为51,这6天分别是几号?
3个数,如果圈出的6个数之和为51,这6天分别是几号?
(2)观察此月历,你还能提出其他的问题吗?
(本题10分)
一方有难,八方支援.2010年4月14日青海玉树发生7.1级强烈地震,给玉树人民
造成了巨大的损失﹒灾难发生后,实验中学举行了爱心捐款活动,全校同学纷纷拿出自己的零花钱, 踊跃捐款支援灾区人民﹒小慧对捐款情况进行了抽样调查,抽取了40名同学的捐款数据,把数据进行分组、列频数分布表后,绘制了频数分布直方图.图中从左到右各长方形高度之比为3∶4∶5∶7∶1(如图).
(1)捐款20元这一组的频数是 ▲;
(2)40名同学捐款数据的中位数是 ▲;
(3)若该校捐款金额不少于34500 元,请估算该校捐款同学的人数至少有多少名?
(本题8分)
如图,AB是⊙O的直径,C是 的中点,CE⊥AB于 E,BD交CE于点F.
的中点,CE⊥AB于 E,BD交CE于点F.
(1)求证:CF﹦BF;
(2)若CD ﹦6, AC ﹦8,则⊙O的半径为 ▲,CE的长是 ▲.
(本题8分)
已知二次函数y=ax2+bx-3的图象经过点A(2,-3),B(-1,0).
(1)求二次函数的解析式;
(2)填空:要使该二次函数的图象与x轴只有一个交点,应把图象沿y轴向上平移
▲个单位.
(本题6分)
在一个阳光明媚、清风徐来的周末,小明和小强一起到郊外放风筝﹒他们把风筝放飞后,将两个风筝的引线一端都固定在地面上的C处(如图).现已知风筝A的引线(线段AC)长20m,风筝B的引线(线段BC)长24m,在C处测得风筝A的仰角为60°,风筝B的仰角为45°.
(1)试通过计算,比较风筝A与风筝B谁离地面更高?
(2)求风筝A与风筝B的水平距离. (精确到0.01 m;)
(本题6分)
如图,在△ABC中,D是BC边上的点(不与B,C重合),F,E分别是AD及其延长线上的点,CF∥BE. 请你添加一个条件,使△BDE≌△CDF (不再添加其它线段,不再标注或使用其他字母),并给出证明.
(1)你添加的条件是: ▲;
(2)证明: