认定：若等比数列
的公比q满足
，则它的所有项的和
，设
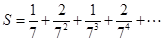。则
（ ）
A． |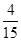
B． |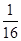
C． |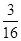
D． |
若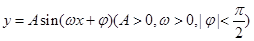
的最小值为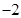
，其图像相邻最高点与最低点横坐标之差为
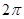，且图像过点（0，1），则其解析式是（）
A． |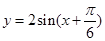
B． |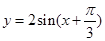
C． |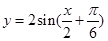
D． |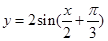
如图是一个算法的程序框图，该算法输出的结果是 （）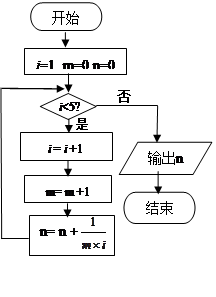
A． |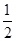
B． |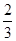
C． |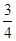
D． |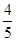
已知向量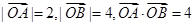
则以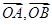
为邻边的平行四边形的面积为（）
A． |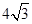
B． |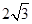
C．4 | D．2 |
设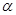
和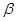
是两个不重合的平面，给出下列命题：
①若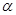外一条直线
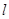与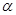内一条直线平行，则
；
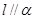②若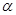内两条相交直线分别平行于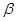内的两条直线 ，则
；
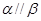③设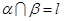
，若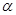内有一条直线垂直于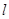，则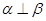
；
④若直线
与平面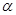内的无数条直线垂直,则
.
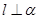上面的命题中，真命题的序号是（ ）
| A．①③ | B．②④ | C．①② | D．③④ |
已知条件
，条件
，则
是
的（）
| A．充分不必要条件 | B．必要不充分条件 |
| C．充要条件 | D．既不充分也不必要条件 |