（本题12分）
提高过立交桥的车辆通行能力可改善整个城市的交通状况．在一般情况下，成都某立交桥上的车流速度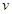
（单位：千米/小时）是车流密度
（单位：辆/千米）的函数．当桥上的车流密度达到200辆/千米时，造成堵塞，此时车流速度为0；当车流密度不超过20辆/千米时，车流速度为60千米/小时．研究表明：当
时，车流速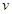度是车流密度的一次函数．
（Ⅰ）当时，求函数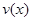
的表达式；
（Ⅱ）当车流密度为多大时，车流量（单位时间内通过桥上某观测点的车辆数，单位：辆/小时）
可以达到最大，并求出最大值．（精确到1辆/小时）
(本小题12分)如图, 一个圆锥形的空杯子上面放着一个半球形的冰淇淋,假设冰淇淋融化后体积不变,是否会溢出杯子? 请说明理由.请用你的计算数据说明理由。（冰、水的体积差异忽略不计）（π取3.14）
已知
=
是矩阵M=
属于特征值λ1=2的一个特征向量．
（Ⅰ）求矩阵M；
（Ⅱ）若
，求M10a．
选修4﹣2：矩阵与变换
已知二阶矩阵M有特征值λ1=4及属于特征值4的一个特征向量
=（
），并有特征值λ2=﹣1及属于特征值﹣1的一个特征向量
=（
），
=（
）．
（1）求矩阵M；
（2）求M5α．
给定矩阵
，
；求A4B．
已知矩阵M=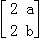
的两个特征值分别为λ1=﹣1和λ2=4．
（1）求实数a，b的值；
（2）求直线x﹣2y﹣3=0在矩阵M所对应的线性变换作用下的象的方程．