在平面直角坐标系中,定义 为两点
为两点 ,之间的“折线距离”.在这个定义下,给出下列命题:
,之间的“折线距离”.在这个定义下,给出下列命题:
①到原点的“折线距离”等于1的点的集合是一个正方形;
②到原点的“折线距离”等于1的点的集合是一个圆;
③到 两点的“折线距离”之和为4的点的集合是面积为6的六边形;
两点的“折线距离”之和为4的点的集合是面积为6的六边形;
④到 两点的“折线距离”差的绝对值为1的点的集合是两条平行线.
两点的“折线距离”差的绝对值为1的点的集合是两条平行线.
其中正确的命题是___________.(写出所有正确命题的序号)
设面积为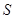 的平面四边形的第
的平面四边形的第 条边的边长记为
条边的边长记为 ,
, 是该四边形内任意一点,
是该四边形内任意一点, 点到第
点到第 条边的距离记为
条边的距离记为 ,若
,若 , 则
, 则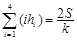 类比上述结论,体积为
类比上述结论,体积为 的三棱锥的第
的三棱锥的第 个面的面积记为
个面的面积记为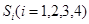 ,
, 是该三棱锥内的任意一点,
是该三棱锥内的任意一点, 点到第
点到第 个面的距离记为
个面的距离记为 ,则相应的正确命题是:若
,则相应的正确命题是:若 ,则.
,则.
 名乒乓球队员中,有
名乒乓球队员中,有 名老队员和
名老队员和 名新队员.现从中选出
名新队员.现从中选出 名队员排成
名队员排成 号参加团体比赛,则入选的
号参加团体比赛,则入选的 名队员中至少有一名老队员,且
名队员中至少有一名老队员,且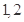 号中至少有
号中至少有 名新队员的排法有______种.(以数字作答)
名新队员的排法有______种.(以数字作答)
已知函数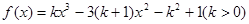 ,若
,若 的单调减区间是(0,4),则在曲线
的单调减区间是(0,4),则在曲线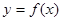 的切线中,斜率最小的切线方程是___________
的切线中,斜率最小的切线方程是___________
若函数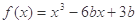 在
在 内有极小值,求实数
内有极小值,求实数 的取值范围是
的取值范围是
某毕业生参加人才招聘会,分别向甲、乙两个公司投递了个人简历,假定该毕业生得到甲公司面试的概率为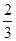 ,得到乙公司面试的概率为
,得到乙公司面试的概率为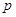 ,且两个公司是否让其面试是相互独立的。记X为该毕业生得到面试得公司个数。若
,且两个公司是否让其面试是相互独立的。记X为该毕业生得到面试得公司个数。若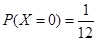 ,则随机变量X的数学期望
,则随机变量X的数学期望