掷一枚正方体的骰子,各个面上分别标有数字1, 2,3,4,5,6,求下列事件发生的可能性的大小:
(1)朝上的数字是奇数;
(2)朝上的数字能被3除余1;
(3)朝上的数字不是3的倍数;
(4)朝上的数字小于6;
(5)朝上的数字不小于3.
如图:AC与BD交于P点,PA=PB=PC=PD.已知△PAB的三点坐标为A(2,2),B(6,2),P(4,5).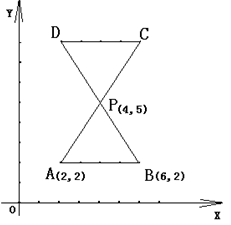
(1)求出C,D的坐标;
(2)将△PAB沿AC方向平移,使P与C重合,则平移后的A,B点的坐标.
如图是重百商场的各个柜台分布平面示意图,请建立合适的直角坐标系,标出各个柜台的坐标. 
平行四边形ABCD,AD=6,AB=8,点A的坐标为(-3,0),求B、C、D各点的坐标。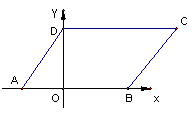
在直角坐标系中,四边形ABCD各个顶点的坐标分别为A(0,0),B(3,6),C(7,8),D(12,0),求四边形ABCD的面积.
如图,在下面的平面直角坐标系中,先画出以A(-2,3),B(-2,-3),C(-3.5,0)三点为顶点的三角形,再画出△ABC关于y轴对称的△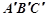 .
.