如图所示，电动机牵引一根原来静止的、长L为1m、质量m为0.1kg的导体棒MN上升，导体棒的电阻R为1Ω，架在竖直放置的框架上，它们处于磁感应强度B为1T的匀强磁场中，磁场方向与框架平面垂直．当导体棒上升h＝3.8m时，获得稳定的速度，导体棒上产生的热量为2J，电动机牵引棒时，电压表、电流表的读数分别为7V、1A，电动机内阻r为1Ω，不计框架电阻及一切摩擦，
求：（1）电动机的输出功率？
（2）导体棒达到稳定时的速度？
（3）导体棒从静止至达到稳定速度所需要的时间？
在竖直平面内建立xoy直角坐标系，oy表示竖直向上方向．如图所示．已知该平面内存在沿x轴正向的区域足够大的匀强电场．一带电小球从坐标原点o沿ox方向以4J的初动能竖直向上抛出．不计空气阻力，它到达的最高位置如图中M点所示，求：
(1)小球在M点时的动能EkM．
(2)设小球落回跟抛出点在同一水平面时的位置为N，求小球到达N点时的动能EkN．
一个电阻元件两端电压是1.5V时，通过它的电流是4.5mA，如果在元件允许的范围内，这个电阻元件两端加的电压为24V时，20秒内有多少电子通过这个电阻器？
质量为m，带电荷量为-q的微粒（重力不计），在匀强电场中的A点时速度为v，方向与电场线垂直，在B点 时速度大小为2V，如图所示，已知A、B两点间的距离为d．求：
（1）A、B两点的电压； （2）电场强度的大小和方向．
如图所示，在不带电的半径为R的导体球附近一点A处，从无限远处移来一点电荷，点电荷的电荷量为q，若A点到球面的距离为L，当达到静电平衡时，导体球上的感应电荷在球心O处产生的场强的大小等于多少？其方向如何？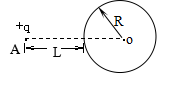
有一个灵敏的电流表它指针满偏时通过的电流Ig=100μA，该表自身的电阻
，欲把这块表接到3V的电路中，又不便该表因为电压过大而烧毁，应将该表串联一个阻值
是多大的电阻？