一质量为2kg的物体在4N的水平拉力作用下由静止开始在水平面上运动,已知物体与水平面之间的动摩擦因数为0.1求:
(1)运动后通过0.5m位移时,物体的速度有多大?
(2)为使它在运动0.5m位移时的速度大小恰好等于0.5m/s,可同时再对物体施加一个竖直向下的力F,则F为多大?(g取10m/s2)
如图所示,在光滑水平面上放着一个质量M=0.3kg的木块(可视为质点),在木块正上方1m处有一个固定悬定点O,在悬点O和木块之间用一根长2m、不可伸长的轻绳连接。有一颗质量m=0.1kg的子弹以80m/s的速度水平射入木块并留在其中,之后木块绕O点在竖直平面内做圆周运动。求:
①木块以多大速度脱离水平地面?
②当木块到达最高点时对轻绳的拉力F为多少?
桌面上有一玻璃圆锥,圆锥的轴(图中虚线)与桌面垂直,过轴线的截面为等边三角形,此三角形的边长为L,如图所示,有一半径为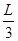 的圆柱形平行光束垂直底面入射到圆锥上,光束的中心轴与圆锥的轴重合。已知玻璃的折射率为
的圆柱形平行光束垂直底面入射到圆锥上,光束的中心轴与圆锥的轴重合。已知玻璃的折射率为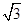 ,求:
,求:
①光在玻璃中的传播速度是多少?
②光束在桌面上形成的光斑的面积是多少?
在图所示的气缸中封闭着温度为100℃的空气,一重物用绳索经滑轮与缸中活塞相连接,重物和活塞均处于平衡状态, 这时活塞离缸底的高度为10 cm,如果缸内空气变为 0℃,问:
①重物是上升还是下降?
②这时重物将从原处移动多少厘米?(设活塞与气缸壁间无摩擦)
一圆筒的横截面如图所示,其圆心为O。筒内有垂直于纸面向里的匀强磁场,磁感应强度为B。圆筒下面有相距为d的平行金属板M、N,其中M板带正电荷,N板带等量负电荷。质量为m、电荷量为q的带正电粒子自M板边缘的P处由静止释放,经N板的小孔S以速度v沿半径SO方向射入磁场中,粒子与圈筒发生两次碰撞后仍从S孔射出,设粒子与圆筒碰撞过程中没有动能损失,且电荷量保持不变,在不计重力的情况下,求:
(1)M、N间电场强度E的大小;
(2)圆筒的半径R;
(3)保持M、N间电场强度E不变,仅将M板向上平移 ,粒子仍从M板边缘的P处由静止释放粒子自进入圆筒至从S孔射出期间,与圆筒的碰撞次数n。
,粒子仍从M板边缘的P处由静止释放粒子自进入圆筒至从S孔射出期间,与圆筒的碰撞次数n。
一个质量为50kg木箱A,放在水平地面上,要将它运送到90m远处的施工现场。如果用450N的水平恒力使A从静止开始运动,经过6s钟可到达施工现场。
(1)求木箱与地面间的动摩擦因数。
(2)若用大小为450N,方向与水平方向夹角为α(cosα=0.8)斜向上的拉力拉木箱A从静止开始运动,使木箱A能够到达90m远处的施工现场,拉力至少做多少功?(运动过程中动摩擦因数处处相同,取 ,结果保留2位有效数字)。
,结果保留2位有效数字)。