(本小题满分12分)已知函数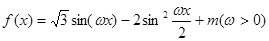 的最小正周期为
的最小正周期为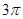 ,当
,当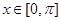 时,函数
时,函数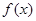 的最小值为0。
的最小值为0。
(1)求函数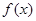 的表达式;
的表达式;
(2)在△ ,若
,若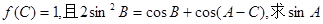 的值。
的值。
(本小题满分14分)
设函数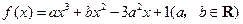 在
在 ,
,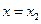 处取得极值,且
处取得极值,且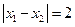 .
.
(Ⅰ)若 ,求
,求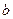 的值,并求
的值,并求 的单调区间;
的单调区间;
(Ⅱ)若 ,求
,求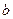 的取值范围.
的取值范围.
(本小题满分12分)
已知命题 在[-1,1]上有解,
在[-1,1]上有解,
命题q:只有一个实数x满足:
(I)若 的图象必定过两定点,试写出这两定点的坐标.
的图象必定过两定点,试写出这两定点的坐标.
(只需写出两点坐标即可,不要过程);
(Ⅱ)若命题“p或q”为假命题,求实数a 的取值范围。
(本小题满分12分)
设函数
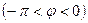 ,
,  图象的一条对称轴是直线
图象的一条对称轴是直线 .
.
(I)求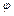 ;
;
(II)求函数 的单调增区间;
的单调增区间;
(Ⅲ)画出函数 在区间
在区间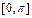 上的图象.
上的图象.
(本小题满分12分)
某小区要建一座八边形的休闲小区,它的主体造型的平面图是由二个相同的矩形ABCD和EFGH构成的面积为200m2的十字型地域,计划在正方形MNPQ上建一座“观景花坛”,造价为4 200元/m2,在四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为210元/m2,再在四个空角(如△DQH等)上铺草坪,造价为80元/m2.
(1)设总造价为S元,AD长为 m,试建立S与x的函数关系;
m,试建立S与x的函数关系;
(2)当x为何值时,S最小?并求这个最小值.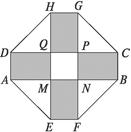
(本小题满分12分)
已知函数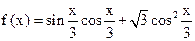 .
.
(I)将函数f(x)写成f(x)= (
(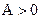 )的形式,并求其图像对称中心的横坐标;
)的形式,并求其图像对称中心的横坐标;
(Ⅱ)如果△ABC的三边a、b、c所对的角分别为A ,B ,C且满足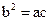 ,且边b所对的角为B,试求角B的取值范围及此时函数f(B)的值域.
,且边b所对的角为B,试求角B的取值范围及此时函数f(B)的值域.