据报道，一儿童玩耍时不慎从H=45m高的阳台上无初速掉下，在他刚掉下时恰被楼下一管理员发现，该管理员迅速由静止冲向儿童下落处的正下方楼底，准备接住儿童．已知管理员到楼底的距离为18m，为确保安全能稳妥接住儿童，管理员将尽力节约时间，但又必须保证接儿童时没有水平方向的冲击，不计空气阻力，将儿童和管理员都看做质点，设管理员奔跑过程中只做匀速或匀变速运动，g取10m/s2．问：
（1）管理员至少用多大的平均速度跑到楼底？
（2）若管理员在加速或减速的加速度大小相等，且最大速度不超过9m/s，求管理员奔跑时加速度需满足什么条件？
用200N的拉力将地面上一个质量为10kg的物体加速提升10m至A点，空气阻力忽略不计。g取
。求：（1）这一过程中重力对物体所做的功。（2）这一过程中拉力对物体所做的功。（3）物体在A点具有的动能。
将小球从距地面0.8m高处以
的速度水平抛出， g取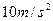
。求小球在空中运动的时间和落地时速度的大小.
某压力锅结
构如图所示。盖好密封锅盖，将压力阀套在出气孔上，给压力锅加热，当锅内气体压强达到一定值时，气体就把压力阀顶起。假定在压力阀被顶起时，停止加热。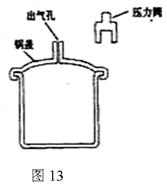
（1）若此时锅内气体的体积为V，摩尔体积为V0，阿伏加德罗常数为NA，写出锅内气体分子数的估算表达式。
（2）假定在一次放气过程中，锅内气体对压力阀及外界做功1 J,并向外界释放了2 J的热量。锅内原有气体的内能如何变化？变化了多少？
（3）已知大气压强P随海拔高度H的变化满足P＝P0（1－αH），其中常数α＞0。结合气体定律定性分析在不同的海拔高度使用压力锅，当压力阀被顶起时锅内气体的温度有何不同。
如图（a）所示，一个电阻值为R ，匝数为n的圆形金属线与阻值为2R的电阻R1连结成闭合回路。线圈的半径为r1 . 在线圈中半径为r2的圆形区域存在垂直于线圈平面向里的匀强磁场，磁感应强度B随时间t变化的关
系图线如图（b）所示。图线与横、纵轴的截距分别为t0和B0。导线的电阻不计
。求0至t1时间内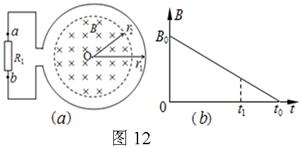
（1）通过电阻R1上的电流大小和方向；
（2）通过电阻R1上的电量q及电阻R1上产生的热量。
一个匝数为n =200的矩形线圈abcd位于匀强磁场中，磁感强度大小为B =0.8T、初始位置如图11所示（线圈平面和磁场方向平行），线圈以ab为轴匀速转动，角速度为ω=5rad/s，已知ab边L1 =15cm，ad边L2 =10cm，线圈的总电阻是R =100Ω。求：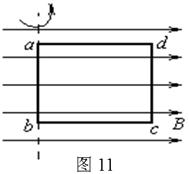
（1）线圈转动过程中的感应电动势的最大值；
（2）线圈从初始位置开始计时，线圈转动过程中的感应电流的瞬时表达式；
（3）线圈从初始位置开始，转过90°角的过程中，通过导线截面的电量；
（4）线圈转动1分钟内外力所做的功。