四棱锥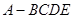 的侧面
的侧面 是等边三角形,
是等边三角形,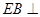 平面
平面 ,
,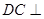 平面
平面 ,
,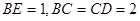 ,
,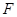 是棱
是棱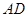 的中点.
的中点.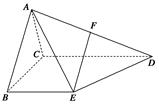
(1)求证: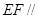 平面
平面 ;
;
(2)求四棱锥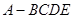 的体积.
的体积.
已知二次函数 ,其导函数
,其导函数 的零点为
的零点为 ,
, .
.
(1)若函数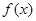 在区间
在区间 上是单调函数,求实数
上是单调函数,求实数 的取值范围;
的取值范围;
(2)若函数 的图象总在函数
的图象总在函数 图象的上方,求
图象的上方,求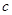 的取值范围.
的取值范围.
等比数列 的前
的前 项和为
项和为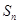 ,已知其公比
,已知其公比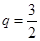 ,
,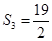 .
.
(1)求数列 的通项公式
的通项公式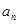 ;
;
(2)求数列 的前
的前 项和
项和 .
.
随着社会的发展,汽车逐步成为人们的代步工具,家庭轿车的保有量逐年上升,交通堵塞现象时有发生,据调查某公路段在某时段内的车流量 (千辆/小时)与汽车的平均速度
(千辆/小时)与汽车的平均速度 (千米/小时)之间有函数关系:
(千米/小时)之间有函数关系: .
.
(1)在该时段内,当汽车的平均速度 为多少时车流量
为多少时车流量 最大?最大车流量为多少?;
最大?最大车流量为多少?;
(2)为保证在该时段内车流量至少为10千辆/小时,则汽车的平均速度应控制在什么范围内?
已知函数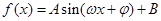 (
( ,
, )的部分图象如图所示,
)的部分图象如图所示,
(1)求函数 的解析式;
的解析式;
(2)若 ,求函数在区间
,求函数在区间 上的最值.
上的最值.
设锐角三角形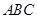 的内角
的内角 、
、 、
、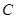 的对边分别为
的对边分别为 、
、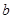 、
、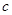 ,且
,且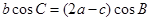 .
.
(1)求 的大小;
的大小;
(2)若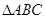 的面积
的面积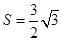 ,
, ,求
,求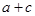 的值.
的值.