两块水平金属极板A、B正对放置,每块极板长均为l、极板间距为d.B板接地(电势为零)、A板电势为+U,重力加速度为g.两个比荷(电荷量与质量的比值)均为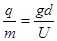 的带正电质点以相同的初速沿A、B板的中心线相继射入,如图所示.第一个质点射入后恰好落在B板的中点处.接着,第二个质点射入极板间,运动一段时间
的带正电质点以相同的初速沿A、B板的中心线相继射入,如图所示.第一个质点射入后恰好落在B板的中点处.接着,第二个质点射入极板间,运动一段时间 后, A板电势突然变为
后, A板电势突然变为 并且不再改变,结果第二个质点恰好没有碰到极板.求:
并且不再改变,结果第二个质点恰好没有碰到极板.求:
(1)带电质点射入时的初速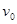 .
.
(2)在A板电势改变之前,第二个质点在板间运动的时间 .
.
某缓冲装置的理想模型如图所示,劲度系数足够大的轻质弹簧与轻杆相连,轻杆可在固定的槽内移动,与槽间的滑动摩擦力恒为f.轻杆向右移动不超过L时,装置可安全工作。轻杆与槽间的最大静摩擦力等于滑动摩擦力,且不计小车与地面的摩擦。一质量为m的小车若以速度v撞击弹簧,将导致轻杆向右移动。
(1)若弹簧的劲度系数为k,求轻杆开始移动时,弹簧的压缩量x
(2)若以速度v0(已知)撞击,将导致轻杆右移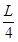 ,求小车与弹簧分离时速度(k未知)
,求小车与弹簧分离时速度(k未知)
(3)在(2)问情景下,求为使装置安全工作,允许该小车撞击的最大速度vm(k未知)
如图所示,一块足够大的光滑平板放置在水平面上,能绕水平固定轴MN调节其与水平面所成的倾角.板上一根长为l=0.60m的轻细绳,它的一端系住一质量为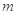 的小球P ,另一端固定在板上的O点.当平板的倾角固定为
的小球P ,另一端固定在板上的O点.当平板的倾角固定为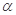 时,先将轻绳平行于水平轴MN拉直,然后给小球一沿着平板并与轻绳垂直的初速度v0=3.0m/s .若小球能保持在板面内作圆周运动,倾角
时,先将轻绳平行于水平轴MN拉直,然后给小球一沿着平板并与轻绳垂直的初速度v0=3.0m/s .若小球能保持在板面内作圆周运动,倾角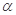 的值应在什么范围内?(取重力加速度g=10m/s2)
的值应在什么范围内?(取重力加速度g=10m/s2)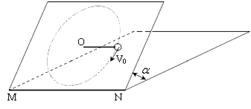
如图所示,在光滑水平地面上,有一质量 的平板小车,小车的右端有一固定的竖直挡板,挡板上固定一轻质细弹簧.位于小车上A点处的质量为
的平板小车,小车的右端有一固定的竖直挡板,挡板上固定一轻质细弹簧.位于小车上A点处的质量为 的木块(视为质点)与弹簧的左端相接触但不连接,此时弹簧与木块间无相互作用力。木块与A点左侧的车面之间有摩擦,与A点右侧的车面之间的摩擦可忽略不计.现小车与木块一起以
的木块(视为质点)与弹簧的左端相接触但不连接,此时弹簧与木块间无相互作用力。木块与A点左侧的车面之间有摩擦,与A点右侧的车面之间的摩擦可忽略不计.现小车与木块一起以 的初速度向右运动,小车将与其右侧的竖直墙壁发生碰撞,已知碰撞时间极短,碰撞后小车以
的初速度向右运动,小车将与其右侧的竖直墙壁发生碰撞,已知碰撞时间极短,碰撞后小车以 的速度水平向左运动,取
的速度水平向左运动,取 .
.
①求小车与竖直墙壁发生碰撞的过程中小车动量变化量的大小;
②若弹簧始终处于弹性限度内,求小车撞墙后与木块相对静止时的速度大小和弹簧的最大弹性势能;
有一顶角为直角的玻璃砖,放在空气中,一光束斜射入玻璃砖的一个侧面,如图所示,然后投射到它的另一个侧面。若该玻璃砖全反射临界角为42°,问:
①这束光线能否从另一侧面射出?
②若光线能从侧面射出,玻璃砖折射率应满足何条件?
如图所示,汽缸放置在水平平台上,活塞质量为10 kg,横截面积为50 cm2,厚度为1 cm,汽缸全长为21 cm,汽缸质量为20 kg,大气压强为1×105 Pa,当温度为7℃时,活塞封闭的气柱长10 cm,若将汽缸倒过来放置时,活塞下方的空气能通过平台上的缺口与大气相通.g取10 m/s2,求: 
(1)汽缸倒置时,活塞封闭的气柱多长;
(2)当温度多高时,活塞刚好接触平台.