(本小题满分14分)已知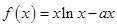 ,
,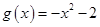 .
.
(1)当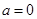 时,求函数
时,求函数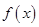 的单调区间;
的单调区间;
(2)对一切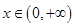 ,
,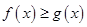 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本小题满分14分)已知椭圆 的中心在原点
的中心在原点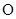 ,焦点在
,焦点在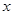 轴上,离心率为
轴上,离心率为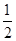 ,右焦点到右
,右焦点到右
顶点的距离为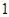 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)是否存在与椭圆 交于
交于 ,
,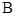 两点的直线
两点的直线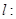
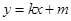 (
( ),使得
),使得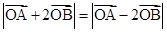
成立?若存在,求出实数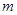 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
(本小题满分14分)已知数列 的前
的前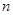 项和为
项和为 ,且
,且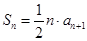 ,其中
,其中 .
.
(1)求数列 的通项公式;
的通项公式;
(2)若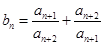 ,数列
,数列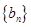 的前
的前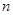 项和为
项和为 ,求证:
,求证: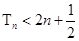 .
.
【改编】(本小题满分14分)在棱锥 中,
中, ,
, 平面
平面 ,
, 平面
平面 ,
, 是
是 的中点,
的中点, ,
, .
.
(1)求证:平面 平面
平面 ;
;
(2)求点 到平面
到平面 的距离.
的距离.
(本小题满分12分)为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对 名六年级学生
名六年级学生
进行了问卷调查得到如下列联表:平均每天喝
 以上为常喝,体重超过
以上为常喝,体重超过
 为肥胖.
为肥胖.
| 常喝 |
不常喝 |
合计 |
|
| 肥胖 |
 |
||
| 不肥胖 |
 |
||
| 合计 |
 |
已知在全部 人中随机抽取
人中随机抽取 人,抽到肥胖的学生的概率为
人,抽到肥胖的学生的概率为 .
.
(1)请将上面的列联表补充完整;
(2)是否有 %的把握认为肥胖与常喝碳酸饮料有关?
%的把握认为肥胖与常喝碳酸饮料有关?
(3)现从常喝碳酸饮料且肥胖的学生中( 名女生),抽取
名女生),抽取 人参加电视节目,则正好抽到一男一女的概率是多少?
人参加电视节目,则正好抽到一男一女的概率是多少?
参考数据:
 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(参考公式: ,其中
,其中 )
)