如图，在平行四边形ABCD中过点A作AE⊥BC，垂足为E，连接DE，F为线段DE上一点且∠AFE＝∠B．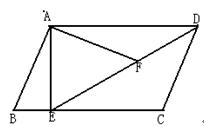
(1)求证：△ADF∽△DEC
(2)若AB＝4,AD＝3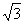
,AE＝3,求AF的长．
计算：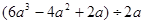
计算：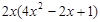
已知：如图，在△ABC中，AB=AC，∠BAC=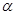
，且60°<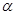<120°．P为△ABC内部一点，且PC=AC，∠PCA=120°—．
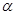（1）用含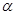的代数式表示∠APC，得∠APC =_______________________；
（2）求证：∠BAP=∠PCB；
（3）求∠PBC的度数．
如图1,给你一张三角形纸片,其中AB="AC," ∠A=36°,将此纸片按图2中的线剪开,可以将原三角形分成三个等腰三角形,那么
（1）仿照图2,再设计两种不同的分割方法,将原三角形纸片分为3个三角形,使得每个三角形都为等腰三角形.
（2）仿照图2,再设计一种不同的分割方法,将原三角形纸片分为4个三角形,使得每个三角形都为等腰三角形.
（要求:在图中标出分得的每个等腰三角形的三个内角的度数）
|
已知在△ABC中，三边长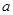
，
，
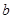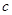满足等式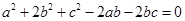
，试判断该三角形是什么三角形，并加以证明．
