已知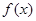 对任意实数
对任意实数 都有
都有 ,且当
,且当 时,
时,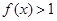 .
.
(1)求证: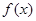 是
是 上的增函数;
上的增函数;
(2)已知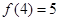 ,解不等式
,解不等式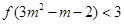 .
.
如图,△ 内接于⊙
内接于⊙ ,
, ,直线
,直线 切⊙
切⊙ 于点
于点 ,弦
,弦 ,
, 相交于点
相交于点 .
.
(Ⅰ)求证:△ ≌△
≌△ ;
;
(Ⅱ)若 ,求
,求 长.
长.
已知 ,点B是
,点B是 轴上的动点,过B作AB的垂线
轴上的动点,过B作AB的垂线 交
交 轴于点Q,若
轴于点Q,若 ,
, .
.
(1)求点P的轨迹方程;
(2)是否存在定直线 ,以PM为直径的圆与直线
,以PM为直径的圆与直线 的相交弦长为定值,若存在,求出定直线方程;若不存在,请说明理由。
的相交弦长为定值,若存在,求出定直线方程;若不存在,请说明理由。
已知椭圆C:  (a>b>0)的两个焦点和短轴的两个端点都在圆
(a>b>0)的两个焦点和短轴的两个端点都在圆 上.
上.
(I)求椭圆C的方程;
(II)若斜率为k的直线过点M(2,0),且与椭圆C相交于A, B两点.试探讨k为何值时,三角形OAB为直角三角形.
如图,在四棱锥 中,底面
中,底面 为菱形,
为菱形, ,
, 为
为 的中点。
的中点。
(1)若 ,求证:平面
,求证:平面 ;
;
(2)点 在线段
在线段 上,
上, ,试确定
,试确定 的值,使
的值,使 ;
;
一个盒子中装有4张卡片,每张卡片上写有1个数字,数字分别是1、2、3、4,现从盒子中随机抽取卡片.
(Ⅰ)若一次从中随机抽取3张卡片,求3张卡片上数字之和大于或等于7的概率;
(Ⅱ)若第一次随机抽取1张卡片,放回后再随机抽取1张卡片,求两次抽取的卡片中至少一次抽到数字2的概率.