(本小题满分12分)
设函数 .
. .
.
(1)当 时,求
时,求 的单调区间;
的单调区间;
(2)若 在
在 上的最大值为
上的最大值为 ,求
,求 的值.
的值.
、已知
(1)求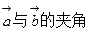

(2)求
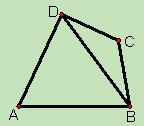
如图,在四边形ABCD中, ,
,
(本小题满分12分)
已知椭圆C: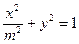 (常数
(常数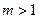 ),P是曲线C上的动点,M是曲线C的右
),P是曲线C上的动点,M是曲线C的右
顶点,定点A的坐标为(2,0).
(1)若M与A重合,求曲线C的焦点坐标.
(2)若 ,求|PA|的最大值与最小值.
,求|PA|的最大值与最小值.
(3)若|PA|最小值为|MA|,求实数 的取值范围.
的取值范围.
(本小题满分12分)
已知函数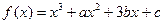 ,
, 且
且 为奇函数.
为奇函数.
(1)求 的值.
的值.
(2)求函数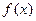 的单调区间
的单调区间
(本小题满分12分)
如图在直三棱柱ABC—A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的
中点.
(1)求证: AC⊥BC1
(2)求证:AC1∥平面CDB1
(3)求异面直线AC1与B1C所成角的余弦值.