已知数列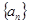 满足:
满足: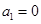 且
且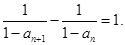 .
.
(1)求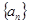 的通项公式;
的通项公式;
(2)令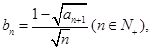 数列
数列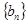 的前n项和为
的前n项和为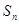 ,证明:
,证明: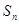 <1.
<1.
如图,A,B是单位圆O上的点,C,D是圆O与x轴的两个交点,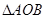 是正三角形.
是正三角形.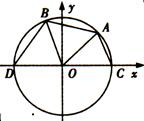
(1)若A点的坐标为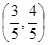 ,求
,求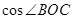 的值;
的值;
(2)若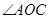 =x
=x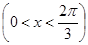 ,四边形CABD的周长为y,试将y表示成x的函数,并求出y的最大值.
,四边形CABD的周长为y,试将y表示成x的函数,并求出y的最大值.
设函数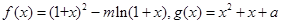 .
.
(1)当a=0时,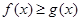 在
在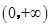 上恒成立,求实数m的取值范围;
上恒成立,求实数m的取值范围;
(2)当m=2时,若函数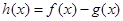 在
在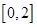 上恰有两个不同的零点,求实数a的取值范围;
上恰有两个不同的零点,求实数a的取值范围;
(3)是否存在常数m,使函数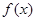 和函数
和函数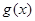 在公共定义域上具有相同的单调性?若存在,求出m的取值范围;若不存在,请说明理由.
在公共定义域上具有相同的单调性?若存在,求出m的取值范围;若不存在,请说明理由.
已知圆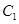 的方程为
的方程为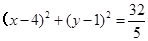 , 椭圆
, 椭圆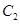 的方程为
的方程为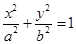 (a>b>0),其离心率为
(a>b>0),其离心率为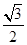 ,如果
,如果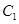 与
与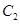 相交于A,B两点,且线段AB恰为圆
相交于A,B两点,且线段AB恰为圆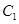 的直径.
的直径.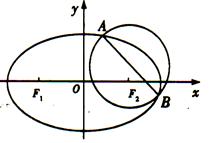
(1)求直线AB的方程和椭圆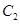 的方程;
的方程;
(2)如果椭圆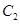 的左,右焦点分别是
的左,右焦点分别是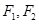 ,椭圆上是否存在点P,使得
,椭圆上是否存在点P,使得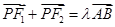 ,如果存在,请求点P的坐标,如果不存在,请说明理由.
,如果存在,请求点P的坐标,如果不存在,请说明理由.
如图,在直三棱柱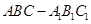 中,AB=AC=5,D,E分别为BC,
中,AB=AC=5,D,E分别为BC, 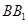 的中点,四边形
的中点,四边形 是边长为6的正方形.
是边长为6的正方形.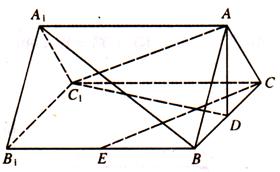
(1)求证: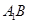 ∥平面
∥平面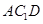 ;
;
(2)求证: ⊥平面
⊥平面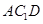 ;
;
(3)求平面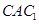 与平面
与平面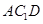 的夹角的余弦值.
的夹角的余弦值.