已知向量 ,
, ,函数
,函数 .
.
(1)求函数 的单调递增区间
的单调递增区间
(2)在 中,
中, 分别是角
分别是角 、
、 、
、 的对边,
的对边, 且
且 ,求
,求 面积
面积 的最大值
的最大值
设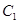 :
: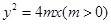 的准线与
的准线与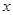 轴交于点
轴交于点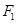 ,焦点为
,焦点为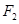 ;椭圆
;椭圆 以
以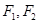 为焦点,离心率
为焦点,离心率 .设
.设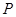 是
是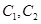 的一个交点.
的一个交点.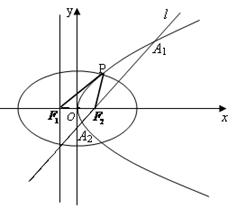
(1)当 时,求椭圆
时,求椭圆 的方程.
的方程.
(2)在(1)的条件下,直线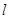 过
过 的右焦点
的右焦点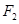 ,与
,与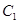 交于
交于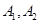 两点,且
两点,且 等于
等于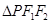 的周长,求
的周长,求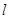 的方程.
的方程.
(3)求所有正实数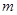 ,使得
,使得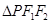 的边长是连续正整数.
的边长是连续正整数.
设 ,用
,用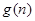 表示
表示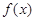 当
当 时的函数值中整数值的个数.
时的函数值中整数值的个数.
(1)求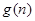 的表达式.
的表达式.
(2)设 ,求
,求 .
.
(3)设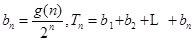 ,若
,若 ,求
,求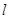 的最小值.
的最小值.
如图,正方体 中,已知
中,已知 为棱
为棱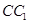 上的动点.
上的动点.
(1)求证: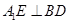 ;
;
(2)当 为棱
为棱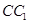 的中点时,求直线
的中点时,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
已知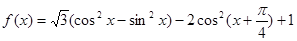 的定义域为[
的定义域为[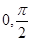 ].
].
(1)求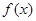 的最小值.
的最小值.
(2)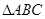 中,
中,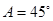 ,
, ,边
,边 的长为函数
的长为函数 的最大值,求角
的最大值,求角 大小及
大小及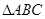 的面积.
的面积.
有驱虫药1618和1573各3杯,从中随机取出3杯称为一次试验(假定每杯被取到的概率相等),将1618全部取出称为试验成功.
(1)求恰好在第3次试验成功的概率(要求将结果化为最简分数).
(2)若试验成功的期望值是2,需要进行多少次相互独立重复试验?