在某校运动会中,甲、乙、丙三支足球队进行单循环赛(即每两队比赛一场)共赛三场,每场比赛胜者得3分,负者得0分,没有平局。在每一场比赛中,甲胜乙的概率为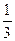 ,甲胜丙的概率为
,甲胜丙的概率为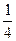 ,乙胜丙的概率为
,乙胜丙的概率为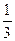 ;
;
(Ⅰ)求甲队获第一名且丙队获第二名的概率;
(Ⅱ)设在该次比赛中,甲队得分为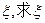 的分布列和数学期望.
的分布列和数学期望.
(本小题满分12分)已知向量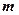
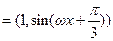 ,向量
,向量
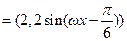 (其中
(其中 为正常数).
为正常数).
(Ⅰ)若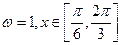 ,求
,求 时
时 的值;
的值;
(Ⅱ)设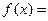
 ,若函数
,若函数 的图像的相邻两个对称中心的距离为
的图像的相邻两个对称中心的距离为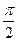 ,求
,求 在区间
在区间 上的最小值.
上的最小值.
已知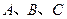 为
为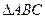 的三内角,且其对边分别为
的三内角,且其对边分别为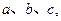 若
若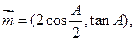
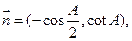 且
且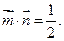
(Ⅰ)求角
(Ⅱ)若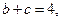
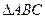 的面积为
的面积为 求
求
设各项为正的数列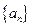 满足:
满足: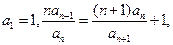 令
令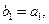
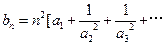
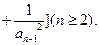
(Ⅰ)求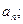
(Ⅱ)求证: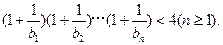
已知曲线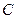 上任意一点
上任意一点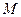 到点
到点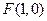 的距离比它到直线
的距离比它到直线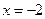 的距离小1.
的距离小1.
(Ⅰ)求曲线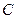 的方程;
的方程;
(Ⅱ)直线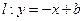 与曲线
与曲线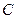 相交于
相交于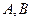 两点,
两点,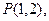 设直线
设直线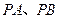 的斜率分别为
的斜率分别为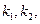
求证: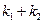 为定值.
为定值.