如图是某种静电分选器的原理示意图.两个竖直放置的平行金属板带有等量异号电荷,形成匀强电场.分选器漏斗的出口与两板上端处于同一高度,到两板距离相等.混合在一起的a、b两种颗粒从漏斗出口下落时,a种颗粒带上正电,b种颗粒带上负电.经分选电场后,a、b两种颗粒分别落到水平传送带A、B上.
已知两板间距d=0.1 m,板的长度l=0.5m,电场仅局限在平行板之间;各颗粒所带电量大小与其质量之比均为1 x10-5G/kg.设颗粒进入电场时的初速度为零,分选过程中颗粒大小及颗粒间的相互作用力不计.要求两种颗粒离开电场区域时,不接触到极板但有最大偏转量,重力加速度g取10m/s2.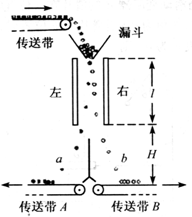
(1)左右两板各带何种电荷?两极板间的电压多大?
(2)若两带电平行板的下端距传送带4、B的高度H=0.3m,颗粒落至传送带时的速度大小是多少?
(3)设颗粒每次与传送带碰撞反弹时,沿竖直方向的速度大小为碰撞前竖直方向速度大小的一半.写出颗粒第n次碰撞反弹高度的表达式.并求出经过多少次碰撞,颗粒反弹的高度小于0.01m.
如图所示,一小型发电站通过升压、降压变压器把电能输送给用户,已知发电机的输出功率为P=500kW,输出电压为U1=500V,升压变压器B1原、副线圈的匝数比为n1:n2=1:5,两变压器间输电导线的总电阻为R=1.5Ω。降压变压器B2的输出电压为U4=220V,不计变压器的损耗。求: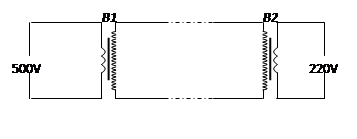
(1)输电导线上损失的功率P';
(2)降压变压器B2的原、副线圈的匝数比n3:n4。
使用回旋加速器的实验需要把离子束从加速器中引出,离子束引出的方法有磁屏蔽通道法和静电偏转法等。质量为
,速度为
的离子在回旋加速器内旋转,旋转轨道时半径为
的圆,圆心在
点,轨道在垂直纸面向外的匀强磁场中,磁感应强度为
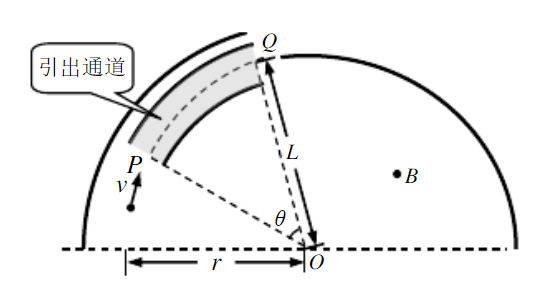
。为引出离子束,使用磁屏蔽通道法设计引出器。引出器原理如图所示,一堆圆弧形金属板组成弧形引出通道,通道的圆心位于
点(
点图中未画出)。引出离子时,令引出通道内磁场的磁感应强度降低,从而使离子从P点进入通道,沿通道中心线从
点射出。已知
长度为
。
与
的夹角为
, 
(1)求离子的电荷量 并判断其正负;
(2)离子从 点进入, 点射出,通道内匀强磁场的磁感应强度应降为 ,求 ;
(3)换用静电偏转法引出离子束,维持通道内的原有磁感应强度 不变,在内外金属板间加直流电压,两板间产生径向电场,忽略边缘效应。为使离子仍从 点进入, 点射出,求通道内引出轨迹处电场强度 的方向和大小。
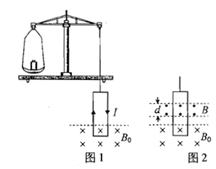
小明同学设计了一个"电磁天平",如图1所示,等臂天平的左臂为挂盘,右臂挂有矩形线圈,两臂平衡。线圈的水平边长
,竖直边长
,匝数为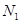 。线圈的下边处于匀强磁场内,磁感应强度
。线圈的下边处于匀强磁场内,磁感应强度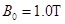 ,方向垂直线圈平面向里。线圈中通有可在
范围内调节的电流
。挂盘放上待测物体后,调节线圈中电流使得天平平衡,测出电流即可测得物体的质量。(重力加速度取
,方向垂直线圈平面向里。线圈中通有可在
范围内调节的电流
。挂盘放上待测物体后,调节线圈中电流使得天平平衡,测出电流即可测得物体的质量。(重力加速度取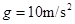 )
)
(1)为使电磁天平的量程达到
,线圈的匝数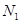 至少为多少。
至少为多少。
(2)进一步探究电磁感应现象,另选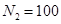 匝、形状相同的线圈,总电阻
匝、形状相同的线圈,总电阻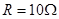 ,不接外电流,两臂平衡,如图2所示,保持
,不接外电流,两臂平衡,如图2所示,保持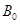 不变,在线圈上部另加垂直纸面向外的匀强磁场,且磁感应强度
随时间均匀变大,磁场区域宽度
不变,在线圈上部另加垂直纸面向外的匀强磁场,且磁感应强度
随时间均匀变大,磁场区域宽度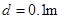 。当挂盘中放质量为
的物体时,天平平衡,求此时磁感应强度的变化率
。当挂盘中放质量为
的物体时,天平平衡,求此时磁感应强度的变化率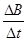 。
。
如图所示,用一块长
的木板在墙和桌面间架设斜面,桌面高
,长
。斜面与水平桌面的倾角
可在
间调节后固定。将质量
的小物块从斜面顶端静止释放,物块与斜面间的动摩擦因数
,物块与桌面间的动摩擦因数
,忽略物块在斜面与桌面交接处的能量损失。(重力加速度取
;最大静摩擦力等于滑动摩擦力) 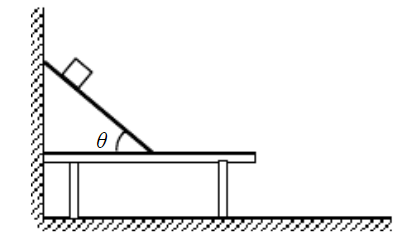
(1)求 角增大到多少时,物块能从斜面开始下滑;(用正切值表示)
(2)当 增大到 时,物块恰能停在桌面边缘,求物块与桌面间的动摩擦因数 ;(已知 , )
(3)继续增大 角,发现 时物块落地点与墙面的距离最大,求此最大距离 。
一台质谱仪的工作原理如图所示,电荷量均为
、质量不同的离子飘入电压为
的加速电场,其初速度几乎为零,这些离子经过加速后通过狭缝
沿着与磁场垂直的方向进入磁感应强度为
的匀强磁场,最后打在底片上,已知放置底片区域已知放置底片的区域
,且
。某次测量发现
中左侧2/3区域
损坏,检测不到离子,但右侧1/3区域
仍能正常检测到离子. 在适当调节加速电压后,原本打在
的离子即可在
检测到.
(1)求原本打在
中点
的离子质量
;
(2)为使原本打在
的离子能打在
区域,求加速电压U的调节范围;
(3)为了在
区域将原本打在
区域的所有离子检测完整,求需要调节
的最少次数。(取
;
)