如图1，矩形MNPQ中，点E，F，G，H分别在NP，PQ，QM，MN上，若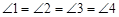
，则称四边形EFGH为矩形MNPQ的反射四边形．图2，图3，图4中，四边形ABCD为矩形，且
，
．
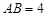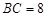理解与作图：
（1）在图2，图3中，点E，F分别在BC，CD边上，试利用正方形网格在图上作出矩形ABCD的反射四边形EFGH．
计算与猜想：
（2）求图2，图3中反射四边形EFGH的周长，并猜想矩形ABCD的反射四边形的周长是否为定值？
启发与证明：
（3）如图4，为了证明上述猜想，小华同学尝试延长GF交BC的延长线于M，试利用小华同学给我们的启发证明（2）中的猜想．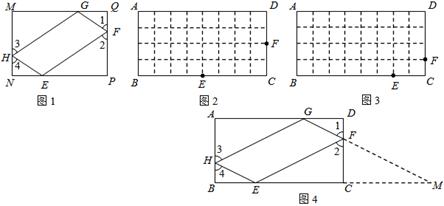
10名学生体检测体重，以50千克为基准，超过的数记为正，不足的数记为负，称得结果如下(单位：千克)：2, 3, －7.5,－3, 5, －8, 3.5, 4.5, 8, －1.5
这10名学生的总体重为多少？10名学生的平均体重为多少？
－55起逐次加上1，得到一连串的数：－54，－53，－52，……，
（1）第100个整数是什么？（2）求这100个整数的和。
如图，这是一个由小立方块塔成的几何体的俯视图，小正方形中的数字表示该位置的小立方块的个数。请你画出它的主视图与左视图。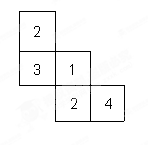
如图，是由7个正方体组成的图案,画出它的主视图、左视图、俯视图.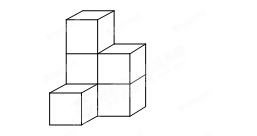
在数轴上表示下列各数：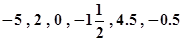
，
，-(-1)，并将它们的相反数用“<”符号连接起来.