在如图所示电路中,R1=390Ω,R2=230Ω,电源内电阻r=50Ω,当K合在1时,电压表的读数为80V;当K合在2时,电压表的读数为U1=72V,电流表的读数为I1=0.18A,求: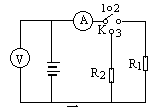
(1)电源的电动势
(2)当K合在3时,两电表的读数。
滑板运动是一项惊险刺激的运动,深受青少年的喜爱。如图11所示,是滑板运动的轨道,AB和CD是一段圆弧形轨道,BC是一段长7m的水平轨道。一运动员从AB轨道上P点以6m/s的速度下滑,经BC轨道后冲上CD轨道,到Q点时速度减为零。已知运动员的质量50kg,h=1.4m,H=1.8m,不计圆弧轨道上的摩擦。求: (g=10m/s2,以水平轨道为零势能面)

(1)运动员第一次经过B点、C点时的速度各是多少?
(2) 运动员与BC轨道的动摩擦因数?
天文学家将相距较近、仅在彼此的引力作用下运行的两颗恒星称为双星.双星系统在银河系中很普遍.利用双星系统中两颗恒星的运动特征可推算出它们的总质量.已知某双星系统中两颗恒星围绕它们连线上的某一固定点分别做匀速圆周运动,周期均为T,两颗恒星之间的距离为r,试推算这个双星系统的总质量.(引力常量为G)
长L=80cm的细绳上端固定,下端系一个质量m=100g的小球。将小球拉起至细绳与竖直方向成60º角的位置,然后无初速释放。如图10所示,不计各处阻力,求小球通过最低点时,小球对细绳拉力多大?(取g=10m/s2)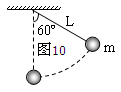
如图9所示,一光滑的半径为R的半圆形轨道(B为最高点,A为最低点)竖直放在水平面上,一个质量为m的小球以某一速度冲上轨道,当小球将要从轨道口飞出时,对轨道的压力恰好为零,则小球落地点C距A处多远?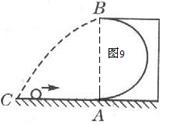
一定质量的理想气体由状态A变为状态D,其有关数据如图甲所示,若状态D的压强是2×104Pa 。求
(1)状态A的压强.
(2)请在乙画中出该状态变化过程的P—T图像,并分别标出A、B、C、D各个状态,不要求写出计算过程。