求证:
已知函数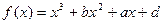 的图象过点P(0,2),且在点M(-1,f(-1))处的切线方程为
的图象过点P(0,2),且在点M(-1,f(-1))处的切线方程为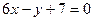 . (Ⅰ)求函数
. (Ⅰ)求函数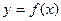 的解析式;
的解析式;
已知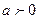 ,n为正整数。设
,n为正整数。设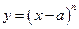 ,证明
,证明 ;
;
(1)设 ,对任意
,对任意 ,证明
,证明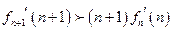
(1)(2005高考北京卷)已知函数f(x)=-x3+3x2+9x+a, (I)求f(x)的单调递减区间;(II)若f(x)在区间[-2,2]上的最大值为20,求它在该区间上的最小值.答案:(1)(-∞,-1),(3,+∞)(2)-7
( 2005全国卷III)已知函数 ,
,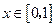 (Ⅰ)求
(Ⅰ)求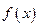 的单调区间和值域;
的单调区间和值域;
(Ⅱ)设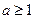 ,函数
,函数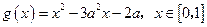 ,若对于任意
,若对于任意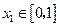 ,总存在
,总存在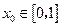 使得
使得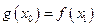 成立,求
成立,求 的取值范围。
的取值范围。
已知椭圆C: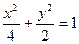 上动点
上动点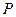 到定点
到定点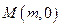 ,其中
,其中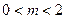 的距离
的距离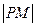 的最小值为1.(1)请确定M点的坐标(2)试问是否存在经过M点的直线
的最小值为1.(1)请确定M点的坐标(2)试问是否存在经过M点的直线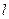 ,使
,使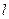 与椭圆C的两个交点A、B满足条件
与椭圆C的两个交点A、B满足条件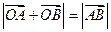 (O为原点),若存在,求出
(O为原点),若存在,求出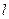 的方程,若不存在请说是理由。
的方程,若不存在请说是理由。