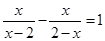某校教师为了对学生零花钱的使用进行教育指导,对全班50名学生每人一周内的零花钱数额进行了调查统计,并绘制了下表
| 零花钱数额/元 |
5 |
10 |
15 |
20 |
| 学生人数 |
10 |
15 |
20 |
5 |
(1)求出这50名学生每人一周内的零花钱数额的平均数、众数和中位数;
(2)你认为(1)中的哪个数据代表这50名学生每人一周零花钱数额的一般水平较为合适?简要说明理由.
如图,在平行四边形ABCD中,已知EF :FC =" 1" :4.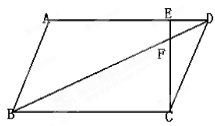
(1)求ED :BC的值;
(2)若AD=8,求AE的长.
如图,已知DE∥BC,CD是∠ACB的平分线,∠B=70°,∠ACB=50°,求∠EDC和∠BDC的度数.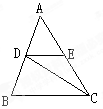
为了了解中学生的体能情况,抽取了某中学八年级学生进行跳绳测试,将所得数据整理后,画出如图所示的频率分布直方图,已知图中从左到右前三个小组的频率分别是0.1,0.3,0.4,第一小组的频数为5。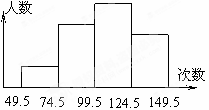
(1)第四小组的频率是__________
(2)参加这次测试的学生是_________人
(3)成绩落在哪组数据范围内的人数最多?是多少?
(4)求成绩在100次以上(包括100次)的学生占测试人数的百分率.
请你先将分式: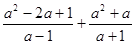 化简,再选取一个你喜欢且使原式有意义的数代入并求值.
化简,再选取一个你喜欢且使原式有意义的数代入并求值.
解方程: