已知:如图1,在面积为3的正方形ABCD中,E、F分别是BC和CD边上的两点,AE⊥BF于点G,且BE=1.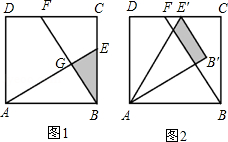
(1)求出△ABE和△BCF重叠部分(即△BEG)的面积;
(2)现将△ABE绕点A逆时针方向旋转到△AB′E′(如图2),使点E落在CD边上的点E′处,问△ABE在旋转前后与△BCF重叠部分的面积是否发生了变化?请说明理由.
如图,点A是反比例函数 图像上的一点,过点A作AB⊥
图像上的一点,过点A作AB⊥ 轴于点B,且△AOB的面积为2,点A的坐标为
轴于点B,且△AOB的面积为2,点A的坐标为 .
.
(1)求m和k的值.
(2)若一次函数y=ax+3的图像经过点A,交双曲线的另一支于点C,交y轴于点D,求△AOC的面积.
(3)在 轴上是否存在点P,使得△PAC的面积为6?如果存在,请求出点P的坐标;若不存在,请说明理由.
轴上是否存在点P,使得△PAC的面积为6?如果存在,请求出点P的坐标;若不存在,请说明理由.
如图,有一段15m长的旧围墙AB,现打算利用该围墙的一部分(或全部)为一边,再利用32m长的篱笆围成一块长方形场地CDEF.
(1)当CD等于多少米时,该场地的面积为126m²?
(2)该场地面积能达到130m²吗?如果能,请求出CD的长度,如果不能,请说明理由.
如图,D是△ABC的边AC上的一点,连接BD,已知∠ABD=∠C,AB=6,AD=4,求线段CD的长.
以“光盘”为主题的公益活动越来越受到社会的关注.某校为培养学生勤俭节约的习惯,随机抽查了部分学生(态度分为:赞成、无所谓、反对),并将抽查结果绘制成图1和图2(统计图不完整).请根据图中提供的信息,解答下列问题:

(1)此次抽样调查中,共抽查了 名学生;
(2)将图1补充完整;
(3)根据抽样调查结果,请你估计该校3000名学生中有多少名学生持反对态度?
海上有一座灯塔P,一客轮以60海里/小时的速度由西向东航行,行至A处时测得灯塔P在北偏东60°方向上,继续航行40分钟到B处,这时测得灯塔P在北偏东30°方向上.已知在灯塔P四周30海里内有暗礁.问这艘船继续向东航行是否安全?