作出函数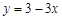 的图象,并根据图象回答下列问题:
的图象,并根据图象回答下列问题:
(1)y的值随x的增大而 ;
(2)图象与x轴的交点坐标是 ;与y轴的交点坐标是 ;
(3)当x 时,y≥0;
(4)函数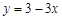 的图象与坐标轴所围成的三角形的面积是________________。
的图象与坐标轴所围成的三角形的面积是________________。
如图,A(-1,0),B(2,-3)两点都在一次函数 与二次函数
与二次函数 的图象上.
的图象上.
(1)求m和二次函数的解析式;
(2)请直接写出当 >
> 时,自变量
时,自变量 的取值范围.
的取值范围.
(3)说出所求的抛物线 可由抛物线y=x2如何平移得到?
可由抛物线y=x2如何平移得到?
如图,点A、B、C分别是⊙O上的点, CD是⊙O的直径,P是CD延长线上的一点,AP=AC.
(1)若∠B=60°,求证:AP是⊙O的切线;
(2)若点B是弧CD的中点,AB交CD于点E,CD=4,求BE·AB的值.
一个不透明的布袋里装有红、黄、绿三种颜色的球(除颜色不同,其它均无任何区别),其中红球2个,黄球1个,绿球1个.
(1)求从袋中任意摸出一个球是红球的概率;
(2)第一次从袋中任意摸出一个球,记下颜色后放回袋中,第二次再摸出一个球记下颜色,请用画树状图或列表的方法求两次都摸到红球的概率(两个红球分别记作红1、红2).
某校要从九年级(1)班和(2)班中各选取10名女同学组成礼仪队,选取的女生的身高(单位:厘米)如下:
(1)班:168 167 170 165 168 166 171 168 167 170
(2)班:165 167 169 170 165 168 170 171 168 167
(1)补充完整下面的统计分析表;
(2)请选一个合适的统计量作为选择标准,说明哪一个班能被选取.
用适当的方法解下列方程
(1)
(2)