如图，在平面直角坐标中，△ABC的三个顶点分别为A（―2，―-优题课

如图，在平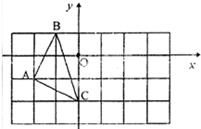面直角坐标中，△ABC的三个顶点分别为A（―2，―1），B（―1，1）C（0，―2）.

（1）点B关于坐标原点O对称的点的坐标为　　　　　　　；
（2）将△ABC绕点C顺时针旋转90°，画出旋转后得到的△A₁B₁C；
（3）求过点B₁的反比例函数的解析式.

科目数学题型解答题难度中等

知识点：对称式和轮换对称式

如图，抛物线 $y = a x^{2} + bx - 2$ 与 $x$ 轴交于 $A$ 、 $B$ 两点，与 $y$ 轴交于 $C$ 点，已知 $A (3, 0)$ ，且 $M (1, - \frac{8}{3})$ 是抛物线上另一点．

（1）求 $a$ 、 $b$ 的值；

（2）连接 $AC$ ，设点 $P$ 是 $y$ 轴上任一点，若以 $P$ 、 $A$ 、 $C$ 三点为顶点的三角形是等腰三角形，求 $P$ 点的坐标；

（3）若点 $N$ 是 $x$ 轴正半轴上且在抛物线内的一动点（不与 $O$ 、 $A$ 重合），过点 $N$ 作 $NH / / AC$ 交抛物线的对称轴于 $H$ 点．设 $ON = t$ ， $ΔONH$ 的面积为 $S$ ，求 $S$ 与 $t$ 之间的函数关系式．

如图，点 $E$ 是正方形 $ABCD$ 的边 $BC$ 延长线上一点，连接 $DE$ ，过顶点 $B$ 作 $BF ⊥ DE$ ，垂足为 $F$ ， $BF$ 分别交 $AC$ 于 $H$ ，交 $CD$ 于 $G$ ．

（1）求证： $BG = DE$ ；

（2）若点 $G$ 为 $CD$ 的中点，求 $\frac{HG}{GF}$ 的值．

某烘焙店生产的蛋糕礼盒分为六个档次，第一档次（即最低档次）的产品每天生产76件，每件利润10元．调查表明：生产每提高一个档次的蛋糕产品，该产品每件利润增加2元．

（1）若生产的某批次蛋糕每件利润为14元，此批次蛋糕属第几档次产品；

（2）由于生产工序不同，蛋糕产品每提高一个档次，一天产量会减少4件．若生产的某档次产品一天的总利润为1080元，该烘焙店生产的是第几档次的产品？

一个口袋中放有290个涂有红、黑、白三种颜色的质地相同的小球．若红球个数是黑球个数的2倍多40个．从袋中任取一个球是白球的概率是 $\frac{1}{29}$ ．

（1）求袋中红球的个数；

（2）求从袋中任取一个球是黑球的概率．

如图，为了测得一棵树的高度 $AB$ ，小明在 $D$ 处用高为 $1 m$ 的测角仪 $CD$ ，测得树顶 $A$ 的仰角为 $45 °$ ，再向树方向前进 $10 m$ ，又测得树顶 $A$ 的仰角为 $60 °$ ，求这棵树的高度 $AB$ ．