(本小题满分12分)
定义在 上的奇函数
上的奇函数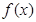 ,已知当
,已知当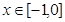 时,
时,
(1)写出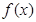 在
在 上的解析式
上的解析式
(2)求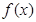 在
在 上的最大值
上的最大值
(3)若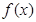 是
是 上的增函数,求实数
上的增函数,求实数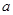 的范围。
的范围。
(本小题满分14分)
设全集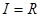 ,已知集合
,已知集合 .
.
(Ⅰ)求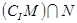 ;(Ⅱ)记集合
;(Ⅱ)记集合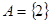 ,已知
,已知 ,
,
若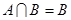 ,求实数
,求实数 的取值范围.
的取值范围.
已知函数 ,
,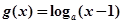 ,其中
,其中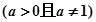 ,设
,设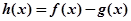 .
.
(Ⅰ) 判断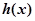 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(Ⅱ)当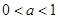 时,判断并证明函数
时,判断并证明函数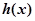 的单调性;
的单调性;
(Ⅲ) 若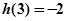 ,且对于区间[3,4]上的每一个x的值,不等式
,且对于区间[3,4]上的每一个x的值,不等式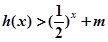
 恒成立,求实数
恒成立,求实数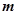 的取值范围.
的取值范围.
已知函数 .
.
(Ⅰ)求函数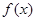 的单调区间;
的单调区间;
(Ⅱ)若把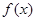 向右平移
向右平移 个单位得到函数
个单位得到函数 ,求
,求 在区间
在区间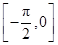 上的最小值和最大值.
上的最小值和最大值.
已知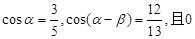 <
<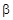 <
<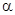 <
<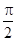 ,
,
(Ⅰ) 求 的值;
的值;
(Ⅱ)求cos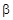 .
.
长虹网络蓝光电视机自投放市场以来,经过两次降价,单价由原来的20000元降到12800元。
(Ⅰ)求这种电视机平均每次降价的百分率,并写出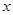 年后该电视的价格
年后该电视的价格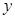 与
与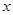 的函数关系式.
的函数关系式.
(Ⅱ)若按(1)中的平均降价百分率计算,问四年后该电视机的价格为多少元?