某市医药公司的甲、乙两仓库分别存有某种药品80箱和70箱，现需要将库存的药品调往A地100箱和B地50箱．
（1）设从甲仓库运送到A地的药品为
箱，请填写下表：
 |
甲仓库 |
乙仓库 |
总计 |
 地 |
箱 |
① 箱 |
100箱 |
 地 |
② 箱 |
③ 箱 |
50箱 |
| 总计 |
80箱 |
70箱 |
150箱 |
（2）已知从甲、乙两仓库运送药品到两地的费用（元／箱）如右表所示．求总费用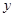
（元）与（箱）之间的函数关系式，并写出的取值范围；
（3）求出最低总费用，并说明总费用最低时的调配方案．
| 地名 |
费用（元/箱） |
|
| 甲库 |
乙库 |
|
| A地 |
14 |
20 |
| B地 |
10 |
8 |
已知△ABC中，∠C=90°，AB=10，AC=6，点O是AB的中点，将一块直角三角板的直角顶点与点O重合并将三角板绕点O旋转，图中的M、N分别为直角三角板的直角边与边AC、BC的交点．
（1）如图①，当点M与点A重合时，求BN的长．
（2）当三角板旋转到如图②所示的位置时，即点M在AC上（不与A、C重合），
①猜想图②中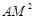
、
、
、
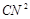之间满足的数量关系式，并说明理由．
②若在三角板旋转的过程中满足CM=CN，请你直接写出此时BN的长．
如图，△ABC中，∠C=90°，AB=5cm，BC=3cm，若动点P从点C开始，按C→A→B的路径运动，且速度为每秒1cm，设出发的时间为t秒．问t为何值时，△BCP为等腰三角形？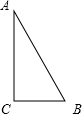
如图，居民楼与马路是平行的，在一楼的点A处测得它到马路的距离为9m，已知在距离载重汽车41m处就可受到噪声影响．
（1）试求在马路上以4m/s速度行驶的载重汽车，能给一楼A处的居民带来多长时间的噪音影响？
（2）若时间超过25秒，则此路禁止该车通行，你认为载重汽车可以在这条路上通行吗？
如图，已知AC平分∠BAD，CE⊥AB于E，CF⊥AD于F，且BC=CD，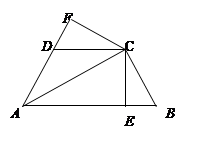
（1）求证：△BCE≌△DCF；
（2）若AB=21，AD=9，AC=17，求CF的长．
已知直线
及其两侧两点A、B，如图．
（1）在直线上求一点P，使PA=PB；
（2）在直线上求一点Q，使平分∠AQB. （以上两小题保留作图痕迹，标出必要的字母，不要求写作法．）