(本小题满分16分)
椭圆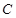 :
: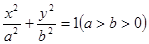 的左、右顶点分别
的左、右顶点分别 、
、 ,椭圆过点
,椭圆过点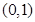 且离心率
且离心率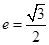 .
.
(1)求椭圆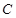 的标准方程;
的标准方程;
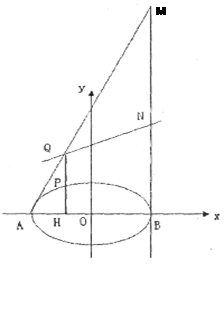
(2)过椭圆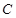 上异于
上异于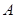 、
、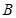 两点的任意一点
两点的任意一点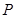 作
作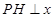 轴,
轴,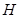 为垂足,延长
为垂足,延长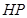 到点
到点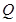 ,且
,且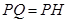 ,过点
,过点 作直线
作直线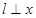 轴,连结
轴,连结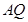 并延长交直线
并延长交直线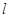 于点
于点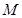 ,线段
,线段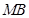 的中点记为点
的中点记为点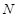 .
.
①求点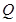 所在曲线的方程;
所在曲线的方程;
②试判断直线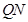 与以
与以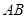 为直径的圆
为直径的圆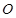 的位置关系, 并证明.
的位置关系, 并证明.
已知点(1, )是函数
)是函数 且
且 )的图象上一点,等比数列
)的图象上一点,等比数列 的前
的前 项和为
项和为 ,数列
,数列
 的首项为
的首项为 ,且前
,且前 项和
项和 满足
满足 -
- =
= +
+ (
( ).
).
(1)求数列 和
和 的通项公式;
的通项公式;
(2)若数列{ 前
前 项和为
项和为 ,问
,问 >
> 的最小正整数
的最小正整数 是多少? .
是多少? .

设 ,
,
(1)令 ,讨论
,讨论 在(0.+∞)内的单调性并求极值;
在(0.+∞)内的单调性并求极值;
(2)求证:当 时,恒有
时,恒有 。
。
已知圆C:x2+y2+2x-4y+3=0;
(1)若圆C的切线在x轴和y轴上的截距相等,求此切线的方程。
(2)从圆C外一点P(x1,y1)向该圆引一条切线,切点为M,O为坐标原点,且有|PM|=|PO|,求使得|PM|取得最小值的点P的坐标。
函数
(1)写出 的单减区间;
的单减区间;
(2)设 最小值为-2,最大值为
最小值为-2,最大值为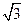 ,求a,b的值。
,求a,b的值。
一个底面为正三角形,且侧棱垂直于底面的棱柱的三视图如图所示,依图 中数据,计算这个的表面积与体积。
中数据,计算这个的表面积与体积。