某同学在做探究弹力和弹簧伸长的关系的实验中,设计了如图所示的实验装置。所用的钩码每只的质量都是30g,他先测出不挂钩码时弹簧的自然长度,再将5个钩码逐个挂在弹簧的下端,每次都测出相应的弹簧总长度,将数据填在了下面的表中。(弹力始终未超过弹性限度,取g=10m/s2)
| 砝码质量(g) |
0 |
30 |
60 |
90 |
120 |
150 |
| 弹簧总长(cm) |
6.00 |
7.15 |
8.34 |
9.48 |
10.64 |
11.79 |
| 弹力大小(N) |
|
|
|
|
|
|
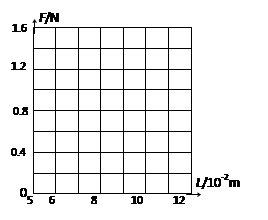
⑴试根据这些实验数据在右图给定的坐标纸上作出弹簧所受弹力大小F跟弹簧总长L之间的函数关系图线,说明图线跟坐标轴交点的物理意义。
⑵上一问所得图线的物理意义?该弹簧的劲度k是多大?(用N/m做单位)
把量程为3mA的电流表改装成欧姆表,其结构如图所示,其中电源电动势E=3V。改装后,将原来电流表3mA的刻度定为电阻的“0”刻度,欧姆表的内阻为Ω,2mA刻度处标为Ω。
在“验证牛顿运动定律”的实验中,在研究加速度a与小车的质量M的关系时,由于没有注意始终满足 M>>m的条件,结果得到的图象应是下图中的 ( )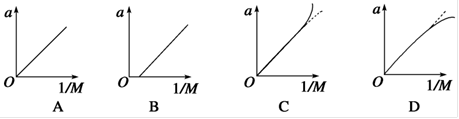
在做“研究匀变速直线运动”的实验时,某同学得到一条用电火花计时器打下的纸带如图甲所示,并在其上取了A、B、C、D、E、F、G 7个计数点,每相邻两个计数点间还有4个点图中没有画出,电火花计时器接220V、 50Hz交流电源。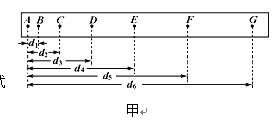
他经过测量并计算得到电火花计时器在打B、C、D、E、F各点时物体的瞬时速度如下表:
| 对应点 |
B |
C |
D |
E |
F |
| 速度(m/s) |
0.141 |
0.180 |
0.218 |
0.262 |
0.301 |
(1)设电火花计时器的周期为T,计算vF的公式为vF=___________;
(2)根据(1)中得到的数据,以A点对应的时刻为t=0,试在图乙所示坐标系中合理地选择标度,作出v-t图象.
(3)利用该图象求物体的加速度a=____________m/s2;
(4)如果当时电网中交变电流的电压变成210V,而做实验的同学并不知道,那么加速度的测量值与实际值相比________(选填:“偏大”、“偏小”或“不变”).
在研究匀变速直线运动的实验中,算出小车经过各计数点的瞬时速度如下:
| 计数点序号 |
1 |
2 |
3 |
4 |
5 |
6 |
| 计数点对应的时刻(s) |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
| 通过计数点的速度(m/s) |
44.0 |
62.0 |
81.0 |
100.0 |
110.0 |
168.0 |
为了计算加速度,最合理的方法是()
| A.根据任意两计数点的速度用公式a=△v/△t算出加速度 |
| B.根据实验数据画出v-t图,量出其倾角,由公式a=tana求出加速度 |
| C.根据实验数据画出v-t图,由图线上相距较远的两点所对应的速度、时间,用公式a=△v/△t算出加速度 |
| D.依次算出通过连续两计数点间的加速度,算出平均值作为小车的加速度 |
在测定匀变速直线运动加速度的实验中,选定一条纸带如图所示,从0点开始,每5个点取一个计数点的纸带,其中0、1、2、3、4、5、6都为记数点。测得:x1=1.40cm,x2=1.90cm,x3=2.38cm,x4=2.88cm,x5=3.39cm,x6=3.87cm。 
(1)在计时器打出点4时,小车的速度分别为:v4=cm/s。
(2) 该匀变速直线运动的加速度的表达式为a=_________________________________,大小a =cm/s2。(结果保留三位有效数字)