某种鲜花进价每束 元,售价每束
元,售价每束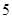 元,若卖不出,则以每束
元,若卖不出,则以每束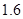 元的价格处理掉。某节日需求量
元的价格处理掉。某节日需求量 (单位:束)的分布列为
(单位:束)的分布列为
 |
200 |
300 |
400 |
500 |
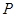 |
 |
 |
 |
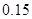 |
(Ⅰ)若进鲜花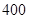 束,求利润
束,求利润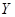 的均值。
的均值。
(Ⅱ)试问:进多少束花可使利润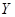 的均值最大?
的均值最大?
某城市计划在如图所示的空地 上竖一块长方形液晶广告屏幕
上竖一块长方形液晶广告屏幕 ,宣传该城市未来十年计划、目标等相关政策.已知四边形
,宣传该城市未来十年计划、目标等相关政策.已知四边形 是边长为30米的正方形,电源在点
是边长为30米的正方形,电源在点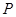 处,点
处,点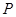 到边
到边 的距离分别为9米,3米,且
的距离分别为9米,3米,且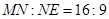 ,线段
,线段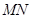 必过点
必过点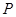 ,端点
,端点 分别在边
分别在边 上,设
上,设 米,液晶广告屏幕
米,液晶广告屏幕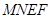 的面积为
的面积为 平方米.
平方米.
(Ⅰ)求 关于
关于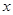 的函数关系式及其定义域;
的函数关系式及其定义域;
(Ⅱ)当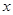 为何值时,液晶广告屏幕
为何值时,液晶广告屏幕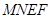 的面积
的面积 最小?
最小?
(Ⅰ)设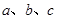 为正数,且
为正数,且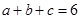 ,求证:
,求证: ;
;
(Ⅱ)设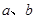 为正数,
为正数, ,求证:
,求证: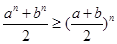
如图,一人在 地看到建筑物
地看到建筑物 在正北方向,另一建筑物
在正北方向,另一建筑物 在北偏西
在北偏西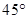 方向,此人向北偏西
方向,此人向北偏西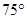 方向前进
方向前进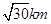 到达
到达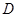 处,看到
处,看到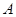 在他的北偏东
在他的北偏东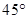 方向,
方向,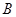 在北偏东
在北偏东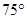 方向,试求这两座建筑物之间的距离.
方向,试求这两座建筑物之间的距离.
.(14分)已知椭圆 +
+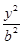 =1(a>b>0)的左、右焦点分别是F1(-c,0),F2(c,0),Q是椭圆外的动点,满足
=1(a>b>0)的左、右焦点分别是F1(-c,0),F2(c,0),Q是椭圆外的动点,满足 =2a.点P是线段F1Q与该椭圆的交点,点T在线段F2Q上,并且满足
=2a.点P是线段F1Q与该椭圆的交点,点T在线段F2Q上,并且满足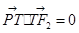 ,
,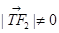
(1)设x为点P的横坐标,证明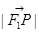 =a+
=a+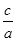 x;
x;
(2)求点T的轨迹C的方程;
(3)试问:在点T的轨迹C上,是否存在点M,使△F1MF2的面积S=b2?若存在,求∠F1MF2的正切值;若不存在,请说明理由.
设二次函数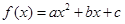 (a>0),方程
(a>0),方程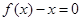 的两个根
的两个根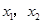
满足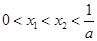 . (1)
. (1) ,求
,求 的值。
的值。
(2)设函数 的图象关于直线
的图象关于直线 对称,证明:
对称,证明:
(3)当x∈(0,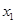 )时,证明x<
)时,证明x< <
<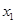 ;
;