.(14分)已知椭圆 +
+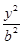 =1(a>b>0)的左、右焦点分别是F1(-c,0),F2(c,0),Q是椭圆外的动点,满足
=1(a>b>0)的左、右焦点分别是F1(-c,0),F2(c,0),Q是椭圆外的动点,满足 =2a.点P是线段F1Q与该椭圆的交点,点T在线段F2Q上,并且满足
=2a.点P是线段F1Q与该椭圆的交点,点T在线段F2Q上,并且满足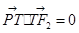 ,
,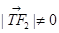
(1)设x为点P的横坐标,证明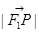 =a+
=a+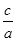 x;
x;
(2)求点T的轨迹C的方程;
(3)试问:在点T的轨迹C上,是否存在点M,使△F1MF2的面积S=b2?若存在,求∠F1MF2的正切值;若不存在,请说明理由.
设函数f ( x ) = 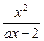 (a ÎN*), 又存在非零自然数m, 使得f (m ) =" m" ,
(a ÎN*), 又存在非零自然数m, 使得f (m ) =" m" ,
f (– m ) < – 成立.
成立.
(1) 求函数f ( x )的表达式;
(2) 设{an}是各项非零的数列, 若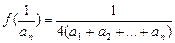 对任意nÎN*成立, 求数列{an}的一个通项公式;
对任意nÎN*成立, 求数列{an}的一个通项公式;
在(2)的条件下, 数列{an}是否惟一确定? 请给出判断, 并予以证明.
.设函数y=f(x)的定义域为(0,+∞),且对任意的正实数x, y,均有
f(xy)=f(x)+f(y)恒成立.已知f(2)=1,且当x>1时,f(x)>0。
(1)求f(1), f(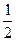 )的值;
)的值;
(2)试判断y=f(x)在(0,+∞)上的单调性,并加以证明;
(3)一个各项均为正数的数列{an}满足f(Sn)=f(an)+f(an+1)-1,n∈N*,其中Sn是数列{an}的前n项和,求数列{an}的通项公式;
(4)在(3)的条件下,是否存在正数M,使2n·a1·a2…an≥M· .(2a1-1)·(2a2-1)…(2an-1)对于一切n∈N*均成立?若存在,求出M的范围;若不存在,请说明理由.
.(2a1-1)·(2a2-1)…(2an-1)对于一切n∈N*均成立?若存在,求出M的范围;若不存在,请说明理由.
.已知二次函数 经过点(0,10),其导数
经过点(0,10),其导数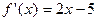 ,当
,当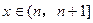 (
(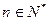 )时,
)时,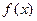 是整数的个数记为
是整数的个数记为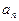 。
。
(1)求数列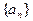 的通项公式;
的通项公式;
(2)令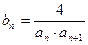 ,求数列
,求数列 的前n项(
的前n项(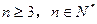 )项和
)项和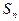 。
。
.已知定义在R上的函数f(x)=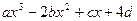 ( a , b , c , d∈R )的图象关于原点对称,且x = 1时,f(x)取极小值
( a , b , c , d∈R )的图象关于原点对称,且x = 1时,f(x)取极小值 。
。
(Ⅰ)求f(x)的解析式;
(Ⅱ)当x∈[-1,1]时,图象旧否存在两点,使得此两面三刀点处的切线互相垂直?试证明你的结论;
(Ⅲ)若 ∈[-1,1]时,求证:| f (
∈[-1,1]时,求证:| f ( )-f(
)-f( )|≤
)|≤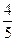 。
。
在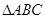 中,
中,
(1)求角B的大小;
(2)求 的取值范围.
的取值范围.