.已知定义在R上的函数f（x）=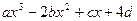
( a , b , c , d∈R )的图象关于原点对称，且x = 1时，f（x）取极小值
。
（Ⅰ）求f（x）的解析式；
（Ⅱ）当x∈[-1，1]时，图象旧否存在两点，使得此两面三刀点处的切线互相垂直？试证明你的结论；
（Ⅲ）若
∈[-1，1]时，求证：| f (
)-f（
）|≤
。
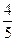（本小题满分12分）
（本小题满分12分）
如图所示茎叶图是青年歌手电视大奖赛中7位评委给参加最后决赛的两位选手甲、乙评定的成绩，程序框图用来编写程序统计每位选手的成绩（各评委所给有效分数的平均值），试根据下面条件回答下列问题：
1）根据茎叶图，乙选手的成绩中，中位数是，众数是。
2）在程序框图中，用k表示评委人数，用a表
示选手的最后成绩（各评委所给有效分数的平均值）那么图中①②处分别为，。“S1=S-max-min”的含义
”。
3）根据程序框图，甲的最后成绩是；乙的最后成绩是。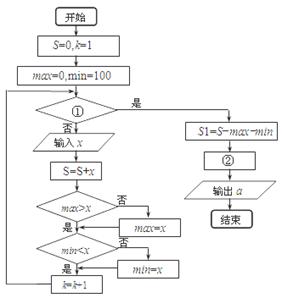
三、解答题:（本大题共5小题，每小题12分，共60分。解答应写出证明过程或演算步骤）
19.（本小题满分12分）
对某校110个小学生进行心理障碍测试得到如下的列联表：
| 焦虑 |
说谎 |
懒惰 |
总计 |
|
| 女生 |
5 |
10 |
15 |
30 |
| 男生 |
20 |
10 |
50 |
80 |
| 总计 |
25 |
20 |
65 |
110 |
通过计算说明在这三种心理障碍中哪一种与性别关系最大？
．是否存在α.β，α∈(－,)，β∈(0,π)，使等式sin(3π－α)＝cos(－β)，cos(－α)＝－cos(π＋β)同时成立？若存在，求出α,β的值，若不存在，
请说明理由．
已知函数f(x)=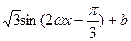
,且该函数图像的对称中心到对称轴的最小距离为
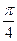当
时,f(x)的最大值为1。
(1) 
求函数f(x)的解析式.
(2) 若f(x)-3≤m≤f(x)+3在
上恒成立,求m的范围.