（本小题满分16分）设二次函数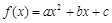
的导函数为
（Ⅰ）若
，且在平面直角坐标系xOy中，直线y=
恰与抛物线y=f（x）相切，求b的值；
（Ⅱ）若
恒成立，
（ⅰ）求证：c≥a＞0；
（ⅱ）求
的最大值．
已知在直角坐标系
中，曲线
为参数，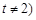
，在以O为极点，x轴
正半轴为极轴的极坐标系中，曲线
，曲线
．
（Ⅰ）求C2与C3交点的直角坐标；
（Ⅱ）若C2与C1相交于点A，C3与C1相交于点B，求
的值．
求与直线
相切于点（3, 4），且在y轴上截得的弦长为
的圆的方程．
在直角坐标系中，以原点为极点，
轴的正半轴为极轴建立坐标系，已知曲线
，过点
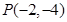的直线
（
为参数）与曲线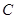
相交于M，N两点．
（1）求曲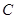线和直线
的普通方程；
（2）若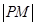
、
、
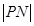成等比数列，求实数
的值．
设函数
．
（1）求
的最大值，并写出使取最大值时
的集合；
（2）已知
中，角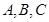
的对边分别为
，若
，
，求
的最小值．
已知函数
的最大值为3，函数
的图象上相邻两对称轴间的距离为
，且
．
（1）求函数的解析式；
（2）将的图象向左平移
个单位，再向下平移1个单位后得到函数
的图象，试判断的奇偶性，并求出在R上的单调递增区间．