如图,三棱锥P—ABC中,PC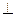 平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD
平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD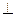 平面PAB.
平面PAB.
(1)求证:AB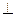 平面PCB;
平面PCB;
(2)求异面直线AP与BC所成角的大小;
(3)求平面PAC和平面PAB所成锐二面角的余弦值.
已知函数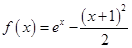 ,
,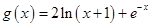 .
.
(1)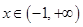 时,证明:
时,证明: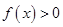 ;
;
(2)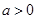 ,若
,若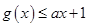 ,求
,求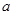 的取值范围.
的取值范围.
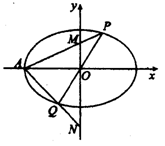
如图,在平面直角坐标系 中,离心率为
中,离心率为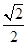 的椭圆
的椭圆
 (
(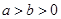 )的左顶点为
)的左顶点为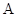 ,过原点
,过原点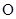 的直线(与坐标轴不重合)与椭圆
的直线(与坐标轴不重合)与椭圆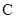 交于
交于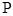 ,
,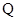 两点,直线
两点,直线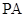 ,
,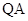 分别与
分别与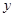 轴交于
轴交于 ,
,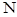 两点.当直线
两点.当直线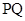 斜率为
斜率为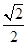 时,
时,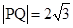 .
.
(1)求椭圆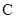 的标准方程;
的标准方程;
(2)试问以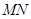 为直径的圆是否经过定点(与直线
为直径的圆是否经过定点(与直线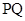 的斜率无关)?请证明你的结论.
的斜率无关)?请证明你的结论.
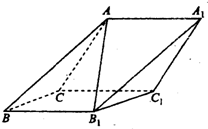
如图,在斜三棱柱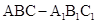 中,侧面
中,侧面 与侧面
与侧面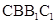 都是菱形,
都是菱形,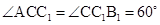 ,
,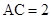 .
.
(1)求证: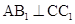 ;
;
(2)若 ,求二面角
,求二面角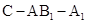 的正弦值.
的正弦值.
现对某市工薪阶层关于“楼市限购令”的态度进行调查,随机抽调了 人,他们月收入的频数分布及对“楼市限购令”赞成人数如下表.
人,他们月收入的频数分布及对“楼市限购令”赞成人数如下表.
| 月收入(单位百元) |
 |
 |
 |
 |
 |
 |
| 频数 |
 |
 |
 |
 |
 |
 |
| 赞成人数 |
 |
 |
 |
 |
 |
 |
(I)由以上统计数据填下面 列联表并问是否有
列联表并问是否有 %的把握认为“月收入以
%的把握认为“月收入以 为分界点”对“楼市限购令”的态度有差异;
为分界点”对“楼市限购令”的态度有差异;
月收入低于 百元的人数 百元的人数 |
月收入低于 百元的人数 百元的人数 |
合计 |
|
| 赞成 |
 |
 |
|
| 不赞成 |
 |
 |
|
| 合计 |
(II)若对月收入在 ,
, 的被调查人中各随机选取两人进行追踪调查,记选中的
的被调查人中各随机选取两人进行追踪调查,记选中的 人中不赞成“楼市限购令”人数为
人中不赞成“楼市限购令”人数为 ,求随机变量
,求随机变量 的分布列及数学期望.
的分布列及数学期望.
参考数据:
 |
 |
 |
 |
 |
 |
 |
 |

在 中,
中,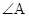 ,
, ,
, 所对的边分别为
所对的边分别为 ,
,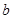 ,
,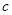 ,若
,若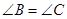 ,且
,且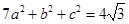 ,求
,求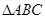 的面积的最大值.
的面积的最大值.