在 中,
中,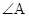 ,
, ,
, 所对的边分别为
所对的边分别为 ,
,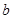 ,
,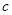 ,若
,若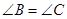 ,且
,且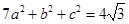 ,求
,求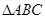 的面积的最大值.
的面积的最大值.
选修4-1:几何证明选讲
如图,AB是⊙O的直径 ,AC是弦 ,∠BAC的平分线AD交⊙O于点D,DE⊥AC,
交AC的延长线于点E.OE交AD于点F.
(1)求证:DE是⊙O的切线;
(2)若 ,求
,求 的值.
的值.
(本小题满分12分)
已知向量 ,
, ,
, ,
,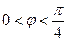 .函数
.函数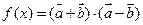 ,若
,若 的图象的一个对称中心与它相邻的一个对称轴之间的距离为1,且过点
的图象的一个对称中心与它相邻的一个对称轴之间的距离为1,且过点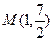 .
.
(Ⅰ)求函数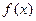 的表达式.
的表达式.
(Ⅱ)当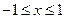 时,求函数
时,求函数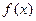 的单调区间.
的单调区间.
(本小题满分12分)
一个四棱锥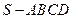 的底面是边长为
的底面是边长为 的正方形,且
的正方形,且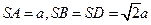 。
。
(1)求证: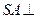 平面
平面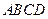 ;
;
(2)若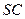 为四棱锥中最长的侧棱,点
为四棱锥中最长的侧棱,点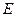 为
为 的中点.求直线SE.与平面SAC所成角的正弦值。
的中点.求直线SE.与平面SAC所成角的正弦值。
(本小题满分12分)
为了研究某高校大学新生学生的视力情况,随机地抽查了该校100名进校学生的视力情况,得到频率分布直方图,如图.已知前4组的频数从左到右依次是等比数列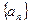 的前四项,后6组的频数从左到右依次是等差数列
的前四项,后6组的频数从左到右依次是等差数列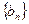 的前六项.
的前六项.
(I)求等比数列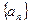 的通项公式;
的通项公式;
(II)求等差数列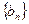 的通项公式;
的通项公式;
(III)若规定视力低于5.0的学生属于近视学生,试估计该校新生的近视率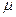 的大小.
的大小.
(本小题满分12分)
已知函数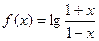 (Ⅰ)求证:对于
(Ⅰ)求证:对于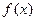 的定义域内的任意两个实数
的定义域内的任意两个实数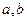 ,都有
,都有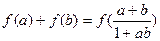 ;(Ⅱ)判断
;(Ⅱ)判断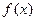 的奇偶性,并予以证明.
的奇偶性,并予以证明.