在△ABC中, .(I)求∠C的大小;(Ⅱ)设角A,B,C的对边依次为
.(I)求∠C的大小;(Ⅱ)设角A,B,C的对边依次为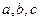 ,若
,若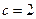 ,且△ABC是锐角三角形,求
,且△ABC是锐角三角形,求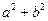 的取值范围.
的取值范围.
已知椭圆 的右焦点为F2(1,0),点
的右焦点为F2(1,0),点 在椭圆上.
在椭圆上.
(1)求椭圆方程;
(2)点 在圆
在圆 上,M在第一象限,过M作圆
上,M在第一象限,过M作圆 的切线交椭圆于P、Q两点,问|F2P|+|F2Q|+|PQ|是否为定值?如果是,求出定值,如不是,说明理由.
的切线交椭圆于P、Q两点,问|F2P|+|F2Q|+|PQ|是否为定值?如果是,求出定值,如不是,说明理由.
在几何体ABCDE中,∠BAC= ,DC⊥平面ABC,EB⊥平面ABC, AB=AC=BE=2,CD=1。
,DC⊥平面ABC,EB⊥平面ABC, AB=AC=BE=2,CD=1。
(1)设平面ABE与平面ACD的交线为直线 ,求证:
,求证: ∥平面BCDE;
∥平面BCDE;
(2)设F是BC的中点,求证:平面AFD⊥平面AFE;
(3)求几何体ABCDE的体积。
已知数列 的前
的前 项和为
项和为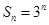 ,数列
,数列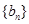 满足:
满足:
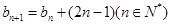 。
。
(1)求数列 的通项公式
的通项公式 ;
;
(2)求数列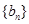 的通项公式
的通项公式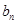 ;
;
(3)若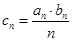 ,求数列
,求数列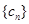 的前
的前 项和
项和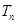 .
.
经销商经销某种农产品,在一个销售季度内,每售出 t该产品获利润
t该产品获利润 元,未售出的产品,每
元,未售出的产品,每 t亏损
t亏损 元。根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示。经销商为下一个销售季度购进了
元。根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示。经销商为下一个销售季度购进了 t该农产品,以
t该农产品,以 (单位:t,
(单位:t, )表示下一个销售季度内的市场需求量,
)表示下一个销售季度内的市场需求量, (单位:元)表示下一个销售季度内销商该农产品的利润。
(单位:元)表示下一个销售季度内销商该农产品的利润。
(1)将 表示为
表示为 的函数;(2)根据直方图估计利润
的函数;(2)根据直方图估计利润 不少于57000元的概率.
不少于57000元的概率.
已知函数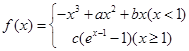 在
在 处存在极值.
处存在极值.
(1)求实数 的值;
的值;
(2)函数 的图像上存在两点A,B使得
的图像上存在两点A,B使得 是以坐标原点O为直角顶点的直角三角形,且斜边AB的中点在
是以坐标原点O为直角顶点的直角三角形,且斜边AB的中点在 轴上,求实数
轴上,求实数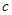 的取值范围;
的取值范围;
(3)当 时,讨论关于
时,讨论关于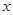 的方程
的方程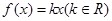 的实根个数.
的实根个数.