（本小题满分13分）双曲线的中心是原点O，它的虚轴长为
，相应于焦点F（c,0）（c＞0）的准线
与x轴交于点A，且|OF|=3|OA|,过点F的直线与双曲线交于P、Q两点.
（1）求双曲线的方程；
（2）若
=0，求直线PQ的方程.
已知函数
的定义域为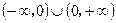
，且满足条件：①
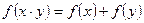，②
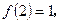③当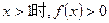
.
（1）求证：函数为偶函数；
（2）讨论函数的单调性；
（3）求不等式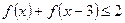
的解集
（本小题満分12分）如图，在四棱锥P—A
BCD中，底面ABCD为矩形，侧棱PA⊥底面ABCD，AB=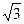
，BC=1，PA=2，E为PD的中点．
（Ⅰ）求直线AC与PB所成角的余弦值；
（Ⅱ）在侧面PAB内找一点N，使NE⊥面PAC，并求出N点到AB和AP的距离．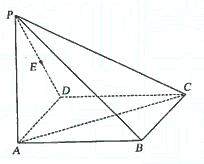
（本小题満分12分）
如图,在正方体ABCD-A1B1C1D1中,E、F分别是BB1、CD的中点．
（Ⅰ）证明AD⊥D1F;
（Ⅱ）求AE与D1F所成的角;
（Ⅲ）证明面AED⊥面A1FD1;
（本小题満分12分）已知中心在原点的双曲线C的右焦点为（2,0），右顶点为
。
（1）求双曲线C的方程；
（2）若直线l：
与双曲线C恒有两个不同的交点A和B，且
（其中O为原点），求k的取值范围。
（本小题満分12分）
已知一条曲线上的每个点M到A（1,0）的距离减去它到y轴的距离差都是1．
（1）求曲线的方程;
（2）讨论直线y=kx+1（k∈R）与曲线的公共点个数