(本小题満分12分)如图,在四棱锥P—A BCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB=
BCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB=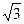 ,BC=1,PA=2,E为PD的中点.
,BC=1,PA=2,E为PD的中点.
(Ⅰ)求直线AC与PB所成角的余弦值;
(Ⅱ)在侧面PAB内找一点N,使NE⊥面PAC,并求出N点到AB和AP的距离.
设函数
(Ⅰ)画出函数
的图像
(Ⅱ)若不等式
的解集非空,求
的取值范围.
已知直线
(
为参数),
(
为参数),
(Ⅰ)当
时,求
与
的交点坐标;
(Ⅱ)过坐标原点
做
的垂线,垂足为
,
为
中点,当
变化时,求
点的轨迹的参数方程,并指出它是什么曲线.
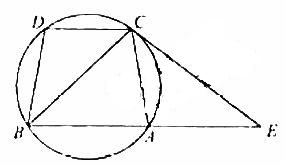
如图,已经圆上的弧
,过
点的圆切线与
的延长线交于
点,证明:
(Ⅰ)
;
(Ⅱ)
.
设函数
。
(1)若
,求
的单调区间;
(2)若当
时
,求
的取值范围.
设
分别是椭圆
的左、右焦点,过
(1)求
(2)设点