（本小题满分16分）已知数列
的奇数项是首项为1的等差数列，偶数项是首项为2的等比数列，数列前n项和为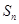
，且满足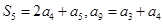
.
（Ⅰ）求数列的通项公式；
（Ⅱ）若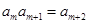
，求正整数m的值；
（Ⅲ）是否存在正整数m，使得
恰好为数列中的一项？若存在，求出所有满足条件的m
值，若不存在，说明理由.
某市
、
、
、
四所中学报名参加某高校今年自主招生的学生人数如下表所示：
| 中学 |
|
|
|
|
| 人数 |
 |
 |
 |
 |
为了了解参加考试的学生的学习状况，该高校采用分层抽样的方法从报名参加考试的四所中学的学生当中随机抽取
名参加问卷调查．
（1）问、、、四所中学各抽取多少名学生？
（2）从参加问卷调查的名学生中随机抽取两名学生，求这两名学生来自同一所中学的概率；
（3）在参加问卷调查的名学生中，从来自、两所中学的学生当中随机抽取两名学生，用
表示抽得中学的学生人数，求的分布列.
设
，
，
.（1）求
的最小正周期、最大值及取最大值时
的集合；
（2）若锐角
满足
，求
的值.
已知数列
的首项
其中
，
令集合
.
（Ⅰ）若
，写出集合
中的所有的元素；
（Ⅱ）若
，且数列中恰好存在连续的7项构成等比数列，求
的所有可能取值构成的集合；
（Ⅲ）求证：
.
已知函数
（Ⅰ）当
时，求曲线
在点
处的切线方程；
（Ⅱ）求
的单调区间；
（Ⅲ）若函数没有零点，求
的取值范围.
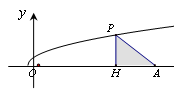
如图，已知点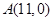
，函数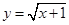
的图象上的动点
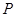在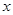
轴上的射影为
，且点在点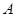
的左侧.设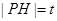
，
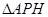的面积为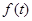
.
（Ⅰ）求函数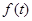的解析式及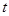
的取值范围；
（Ⅱ）求函数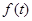的最大值.