(本小题满分16分)如图,在平面直角坐标系 xOy 中,A,B 是圆 O: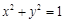 与 x 轴的两个交点(点 B 在点 A右侧),点 Q(-2,0), x 轴上方的动点 P 使直线 PA,PQ,PB 的斜率存在且依次成等差数列.
与 x 轴的两个交点(点 B 在点 A右侧),点 Q(-2,0), x 轴上方的动点 P 使直线 PA,PQ,PB 的斜率存在且依次成等差数列.
(Ⅰ)求证:动点 P 的横坐标为定值;
(Ⅱ)设直线 PA,PB 与圆 O 的另一个交点分别为 S,T,求证:点 Q,S,T 三点共线.
(本小题满分12分)已知函数 ,若存在
,若存在 恒成立,则称
恒成立,则称 的一个“下界函数”.
的一个“下界函数”.
(I)如果函数 的一个“下界函数”,求实数t的取值范围;
的一个“下界函数”,求实数t的取值范围;
(II)设函数 ,试问函数F(x)是否存在零点?若存在,求出零点个数;若不存在,请说明理由.
,试问函数F(x)是否存在零点?若存在,求出零点个数;若不存在,请说明理由.
(本小题满分12分)已知函数
(I)若函数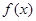 在区间
在区间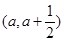 上存在极值,求实数a的取值范围;
上存在极值,求实数a的取值范围;
(II)当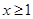 时,不等式
时,不等式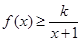 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.
(本小题满分12分)已知数列 的前n项和为
的前n项和为 等差数列
等差数列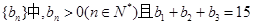 ,又
,又 成等比数列.
成等比数列.
(I)求数列 、
、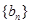 的通项公式;
的通项公式;
(II)求数列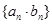 的前n项和
的前n项和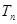 .
.
(本小题满分12分)为征求个人所得税修改建议,某机构对居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在[1000,1500))。
(I)求居民月收入在[3000,4000)的频率;
(II)为了分析居民的收入与年龄、职业等方面的关系,必须按月收入再从这10000人中用分层抽样方法抽出100人作进一步分析,设月收入在[3500,4000)的这段应抽人数为m,求m的值.
(III)若从(II)中被抽取的m人中再选派两人参加一项慈善活动,求其中的甲、乙两人至少有一个被选中的概率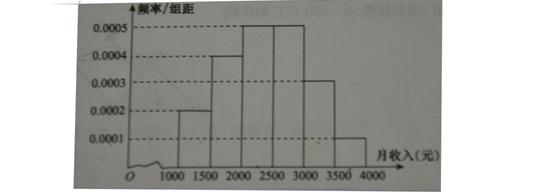
(本小题满分12分)已知函数
(I)求函数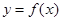 图象的对称轴方程;
图象的对称轴方程;
(II)求函数 的最小正周期和值域.
的最小正周期和值域.