(本小题满分14分)下图是一块平行四边形园地ABCD,经测量,AB=20m,BC=10m,∠ABC=120°.拟过线段AB上一点E设计一条直路EF(点F在四边形ABCD的边上,不计路的宽度),将该园地分为面积之比为3:1的左、右两部分分别种植不同花卉.设EB=x,EF=y(单位:m).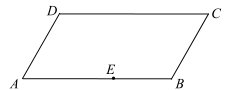
(Ⅰ)当点F与点C重合时,试确定点E的位置;
(Ⅱ)求y关于x的函数关系式;
(Ⅲ)请确定点E,F的位置,使直路EF长度最短.
(本小题满分10分)选修4—5:不等式选讲
设函数
(1)若a=1,解不等式 ;
;
(2)若函数 有最小值,求实数a的取值范围.
有最小值,求实数a的取值范围.
(本小题满分10分)选修4-4:坐标系与参数方程选讲.
在直角坐标系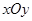 中,曲线
中,曲线 的参数方程为
的参数方程为 (
(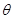 为参数),若以该直角坐标系的原点
为参数),若以该直角坐标系的原点 为极点,
为极点, 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线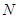 的极坐标方程为:
的极坐标方程为: (其中
(其中 为常数).
为常数).
(1)若曲线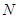 与曲线
与曲线 只有一个公共点,求
只有一个公共点,求 的取值范围;
的取值范围;
(2)当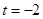 时,求曲线
时,求曲线 上的点与曲线
上的点与曲线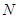 上点的最小距离.
上点的最小距离.
(本小题满分10分)选修4—1:几何证明选讲
如图,AB是 的直径,弦BD、CA的延长线相交于点E,F为BA延长线上一点,且
的直径,弦BD、CA的延长线相交于点E,F为BA延长线上一点,且 ,求证:
,求证: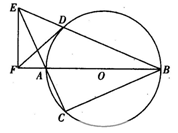
(1)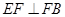 ;
;
(2) .
.
(本小题满分12分)已知函数 .
.
(1)讨论函数 的单调性;
的单调性;
(2)对于任意正实数 ,不等式
,不等式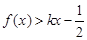 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)是否存在最小的正常数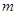 ,使得:当
,使得:当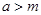 时,对于任意正实数
时,对于任意正实数 ,不等式
,不等式 恒成立?给出你的结论,并说明结论的合理性.
恒成立?给出你的结论,并说明结论的合理性.
(本小题满分12分)已知椭圆 的离心率为
的离心率为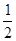 ,椭圆
,椭圆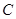 的右焦点
的右焦点 和抛物线
和抛物线
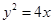 的焦点相同.
的焦点相同.
(1)求椭圆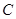 的方程.
的方程.
(2)如图,已知直线
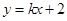 与椭圆
与椭圆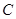 及抛物线
及抛物线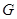 都有两个不同的公共点,且直线
都有两个不同的公共点,且直线 与椭圆
与椭圆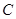 交于
交于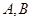 两点;过焦点
两点;过焦点 的直线
的直线 与抛物线
与抛物线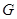 交于
交于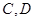 两点,记
两点,记 ,求
,求 的取值范围.
的取值范围.