(本小题满分12分)已知椭圆 的离心率为
的离心率为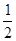 ,椭圆
,椭圆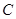 的右焦点
的右焦点 和抛物线
和抛物线
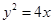 的焦点相同.
的焦点相同.
(1)求椭圆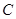 的方程.
的方程.
(2)如图,已知直线
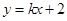 与椭圆
与椭圆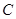 及抛物线
及抛物线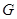 都有两个不同的公共点,且直线
都有两个不同的公共点,且直线 与椭圆
与椭圆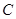 交于
交于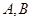 两点;过焦点
两点;过焦点 的直线
的直线 与抛物线
与抛物线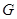 交于
交于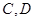 两点,记
两点,记 ,求
,求 的取值范围.
的取值范围.
已知函数 .
.
(Ⅰ)求函数 的最小正周期;
的最小正周期;
(Ⅱ) 求函数 的单调递增区间.
的单调递增区间.
已知:函数 的定义域为
的定义域为 ,集合
,集合 .
.
(Ⅰ)求集合 ;
;
(Ⅱ)求 .
.
已知函数 ,
, 其中
其中
(Ⅰ)若 是函数
是函数 的极值点,求实数
的极值点,求实数 的值;
的值;
(Ⅱ)若对任意的 (
( 为自然对数的底数)都有
为自然对数的底数)都有 成立,求实数
成立,求实数 的取值范围
的取值范围
在平面直角坐标系 中,已知圆心在
中,已知圆心在 轴上,半径为
轴上,半径为 的圆
的圆 位于
位于 轴的右侧,且与
轴的右侧,且与 轴相切,
轴相切,
(Ⅰ)求圆 的方程;
的方程;
(Ⅱ)若椭圆 的离心率为
的离心率为 ,且左右焦点为
,且左右焦点为 ,试探究在圆
,试探究在圆 上是否存在点
上是否存在点 ,使得
,使得 为直角三角形?若存在,请指出共有几个这样的
为直角三角形?若存在,请指出共有几个这样的 点?并说明理由(不必具体求出这些点的坐标)
点?并说明理由(不必具体求出这些点的坐标)
为了调查学生的视力情况,随机抽查了一部分学生的视力,将调查结果分组,分组区间为 ,经过数据处理,得到如下频率分布表
,经过数据处理,得到如下频率分布表
| 分组 |
频数 |
频率 |
 |
3 |
0.06 |
 |
6 |
0.12 |
 |
25 |
 |
 |
 |
 |
 |
2 |
0.04 |
| 合计 |
 |
1.00 |
(Ⅰ)求频率分布表中未知量 ,
, ,
, ,
, 的值
的值
(Ⅱ)从样本中视力在 和
和 的所有同学中随机抽取两人,求两人视力差的绝对值低于
的所有同学中随机抽取两人,求两人视力差的绝对值低于 的概率
的概率