(本小题满分12分)
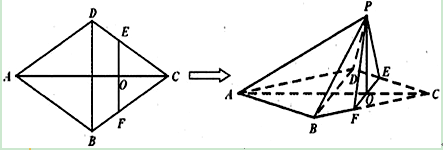
如图,在边长为4的菱形 中,
中, .点
.点 分别在边
分别在边 上,点
上,点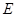 与点
与点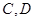 不重合,
不重合,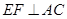 ,
,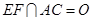 .沿
.沿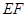 将
将 翻折到
翻折到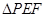 的位置,使平面
的位置,使平面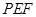 ⊥平面
⊥平面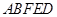 .
.
(1)求证: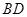 ⊥平面
⊥平面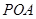 ;
;
(2)当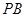 取得最小值时,请解答以下问题:
取得最小值时,请解答以下问题:
(i)求四棱锥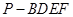 的体积;
的体积;
(ii)若点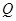 满足
满足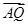 =
=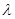
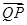 (
(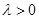 ),试探究:直线
),试探究:直线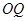 与平面
与平面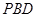 所成角的大小是否一定大于
所成角的大小是否一定大于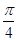 ?并说明理由.
?并说明理由.
设A={x︱x2+4x=0},B={x︱x2+2(a+1)x+ a2-1=0},若A∩ B=B,求a的取值集合。
B=B,求a的取值集合。
(本题11分)如图1,抛物线y=ax2+bx+c(a≠0)的顶点为(1,4),交x轴于A、B,交y轴于D,其中B点的坐标为(3,0)
(1)求抛物线的解析式
(2)如图 2,过点A的直线与抛物线交于点E,交y轴于点F,其中E点的横坐标为2,若直线PQ为抛物线的对称轴,点G为PQ上一动点,则
2,过点A的直线与抛物线交于点E,交y轴于点F,其中E点的横坐标为2,若直线PQ为抛物线的对称轴,点G为PQ上一动点,则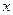 轴上是否存在一点H,使D、G、F、H四点围成的四边形周长最小.若存在,求出这个最小值及G、H的坐
轴上是否存在一点H,使D、G、F、H四点围成的四边形周长最小.若存在,求出这个最小值及G、H的坐 标;若不存在,请说明理由.
标;若不存在,请说明理由.
(3)如图3,抛物线上是否存在一点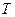 ,过点
,过点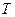 作
作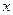 轴的垂线,垂足为
轴的垂线,垂足为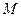 ,过点
,过点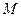 作直线
作直线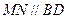 ,交线段
,交线段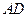 于点
于点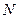 ,连接
,连接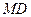 ,使
,使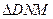 ~
~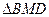 ,若存在,求出点
,若存在,求出点 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.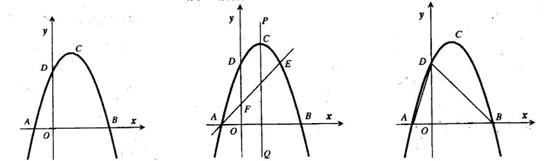 图1图2
图1图2  图3
图3
(本题11分)如图,矩形ABCD中,AB=6,BC=2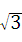 ,点O是AB的中点,点P在AB的延长线
,点O是AB的中点,点P在AB的延长线 上,且BP=3.一动点E从O点出发,以每秒1个单位长度的速度沿OA匀速运动,到达A点后,立即以原速度沿AO返回;另一动点F从P点
上,且BP=3.一动点E从O点出发,以每秒1个单位长度的速度沿OA匀速运动,到达A点后,立即以原速度沿AO返回;另一动点F从P点 出发,以每秒1个单位长度的速度沿射线PA匀速运动,点E、F同时出发,当两点相遇时停止运动,在点E、F的运动过程中,以EF为边作等边△EFG,使△EFG和矩形ABCD在射线PA的同侧.设运动的时间为t秒(t≥0).
出发,以每秒1个单位长度的速度沿射线PA匀速运动,点E、F同时出发,当两点相遇时停止运动,在点E、F的运动过程中,以EF为边作等边△EFG,使△EFG和矩形ABCD在射线PA的同侧.设运动的时间为t秒(t≥0).
(1)当等边△EFG的边FG恰好经过点C时,求运动时间t的值;
(2)在整个运动过程中,设等边△EFG和矩形ABCD重叠部分的面积 为S,求出S与t之间的函数关系式和相应的自变量t的取值范围;
为S,求出S与t之间的函数关系式和相应的自变量t的取值范围;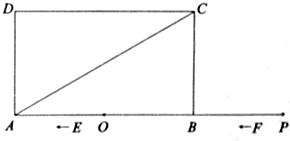
(本 题9分)已知全集
题9分)已知全集 ,集合
,集合 ,
,
集合
(1)是否存在实数 使
使 ,若存在,求出
,若存在,求出 的值;若不存在,说明理由。
的值;若不存在,说明理由。
(2)设有限集合 ,则
,则 叫做集合
叫做集合 的和,记做
的和,记做 .若集合
.若集合 ,集合
,集合 的所有子集分别
的所有子集分别 为
为 求
求
(注: )
)
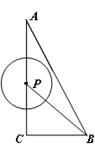
(本题共9分)如图,在△ACB中,∠AC B=90°,AC=4,BC=
B=90°,AC=4,BC= 2,点P为线段CA(不包括端点)上的一个动点,以
2,点P为线段CA(不包括端点)上的一个动点,以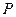 为圆心,1为半径作
为圆心,1为半径作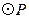 .
.
(1)连结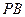 ,若
,若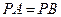 ,试判断
,试判断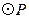 与直线AB的位置关系,并说明理由;
与直线AB的位置关系,并说明理由;
(2)当线段PC等于多少时,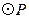 与直线AB相切?
与直线AB相切?
(3)当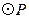 与直线AB相交时,写出线段PC的取值范围。
与直线AB相交时,写出线段PC的取值范围。
(第(3)问直接给出结果,不需要解题过程)