现计划把甲种货物1240吨和乙种货物880吨用一列货车运往某地,已知这列货车挂在A、B两种不同规格的货车厢共40节,使用A型车厢每节费用为6000元,使用B型车厢每节费用为8000元.
(1)设运送这批货物的总费用为y万元,这列货车挂A型车厢x 节,试定出用车厢节数x表示总费用y的公式;
(2)如果每节A型车厢最多可装甲种货物35吨和乙种货物15吨,每节B型车厢最多可装甲种货物25吨和乙种货物35吨,装货时按此要求安排A、B两种车厢的节数,那么共有哪几种安排车厢的方案?
为了加强食品安全管理,有关部门对某大型超市的甲、乙两种品牌食用
油共抽取18瓶进行检测,检测结果分成“优秀”、“合格”、“不合格”三个等级,数据处理
后制成以下折线统计图和扇形统计图.
(1)甲、乙两种品牌食用油各被抽取了多少瓶用于检测?
(2)在该超市购买一瓶乙品牌食用油,请估计能买到“优秀”等级的概率是多少?

如图10所示,Rt△ABC是一张放在平面 直角坐标系中的纸片,点C与原点O重合,点A在x轴的正半轴上,点B在y轴的正半轴上,已知OA=3,OB=4。将纸片的直角部分翻折,使点C落在AB边上,记为D点,AE为折痕,E在y轴上。
直角坐标系中的纸片,点C与原点O重合,点A在x轴的正半轴上,点B在y轴的正半轴上,已知OA=3,OB=4。将纸片的直角部分翻折,使点C落在AB边上,记为D点,AE为折痕,E在y轴上。
(1)在图10所示的直角坐标系中,求E点的坐标及AE的长。
(2)线段AD上有一动点P(不与A、D重合)自A点沿AD方向以每秒1个单位长度向D点作匀速运动,设运动时间为t秒(0<t<3),过P点作PM∥DE交AE于M点,过点M作MN∥AD交DE于N点,求四边形PMND的面积S与时间t之间的函数关系式,当t取何值时,S有最大值?最大值是多少?
(3)当t(0<t<3)为何值 时,A、D、M三点构成等腰三角形?并求出点M的坐标。
时,A、D、M三点构成等腰三角形?并求出点M的坐标。
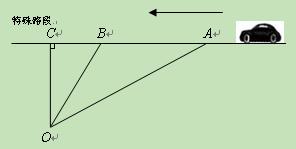
某一特殊路段规定:汽车行驶速度不超过36千米/时。一辆汽车在该路段上由东向西行驶,如图所示,在距离路边10米O处有一“车速检测仪”,测得该车从北偏东600的A点行驶到北偏东300的B点,所用时间为1秒。
(1)试求该车从A点到B点的平均速度。
(2)试说明该车是否超速。(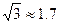 、
、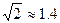 )
)
如图8,已知:△ABC是⊙O的内接三角形,D是OA延 长线上的一点,连接DC,且∠B=∠D=300。
长线上的一点,连接DC,且∠B=∠D=300。
(1)判断直线CD与⊙O的位置关系,并说明理由。
(2)若AC=6,求图中弓形(即阴影部分)的面积。