利用分解因式计算: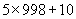 .
.
如图,直线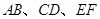 相交于点
相交于点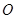 。
。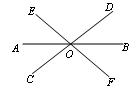
(1)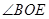 的对顶角是_______。图中共有对顶角对。
的对顶角是_______。图中共有对顶角对。
(2)若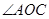
 ,
,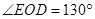 , 求
, 求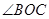 的度数。
的度数。
如图,是由一些大小相同的小正方体组合成的简单几何体.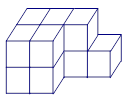
(1)图中有块小正方体;
(2)该几何体的主视图如图所示,请在下面方格纸中分别画出它的左视图和俯视图.


主视图左视图俯视图
解方程
(1)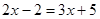 ;
;
(2)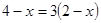 ;
;
(3) 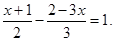
(4) 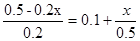
化简求值
(1) 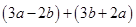
(2)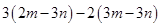
(3)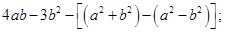 其中a=2,b=-3.
其中a=2,b=-3.
图a是一个长为2 m、宽为2 n的长方形, 沿图中虚线用剪刀均分成四块小长方形, 然后按图b的形状拼成一个正方形。

图a图b
(1)你认为图b中的阴影部分的正方形的边长等于。
(2)请用两种不同的方法求图b中阴影部分的面积。
方法1:方法2:
(3)观察图b,你能写出下列三个代数式之间的等量关系吗?
代数式: 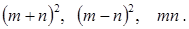
________________________________________
(4)根据(3)题中的等量关系,解决如下问题:
若 ,求
,求 的值。
的值。