图a是一个长为2 m、宽为2 n的长方形, 沿图中虚线用剪刀均分成四块小长方形, 然后按图b的形状拼成一个正方形。
图a 图b
(1)你认为图b中的阴影部分的正方形的边长等于 。
(2)请用两种不同的方法求图b中阴影部分的面积。
方法1： 方法2：
(3)观察图b，你能写出下列三个代数式之间的等量关系吗?
代数式：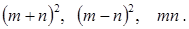 
________________________________________
(4)根据（3）题中的等量关系，解决如下问题：
若
，求
的值。
将分别标有数字1，2，3的三张卡片洗匀后，背面朝上放在桌面上.随机地抽取一张，求抽到的卡片上的数字为偶数的概率；
随机地抽取一张作为十位上的数字（不放回），再抽取一张作为个位上的数字，恰好这个两位数是奇数的概率是多少？
如图，在下面3个正方形格纸中，各有一个以格点为顶点的三角形，请分别在这些格纸中各画一个（三边都画实线）与原三角形成轴对称且也以格点为顶点的三角形.
解不等式组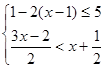
，并把解集在数轴上表示出来．
计算：
．
已知：正方形ABCD的边长为2，⊙O交正方形ABCD的对角线AC所在直线于点T，连结TO交⊙O于点S，连结AS．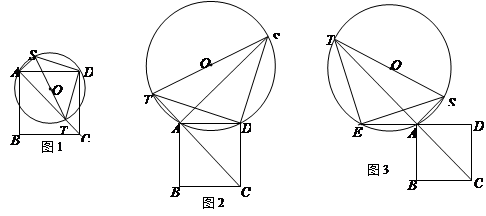
如图1，当⊙O经过A、D两点且圆心O在正方形ABCD内部时，连结DT、DS．
①试判断线段DT、DS的数量关系和位置关系；②求AS＋AT的值；如图2，当⊙O经过A、D两点且圆心O在正方形ABCD外部时，连结DT、DS．求AS－AT的值；
如图3，延长DA到点E，使AE=AD，当⊙O经过A、E两点时，连结ET、ES．
根据（1）、（2）计算，通过观察、分析，对线段AS、AT的数量关系提出问题并解答．